Оператор цикла с предусловием while

Оператор цикла while используется в программе, если надо провести некоторые повторные вычисления (цикл), однако число повторов заранее неизвестно и определяется самим ходом вычисления. В общем виде оператор выглядит так: while условие do begin {последовательность операторов}; end;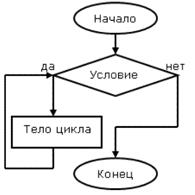

Оператор цикла while работает следующим образом:

Вычисляется условие. Если условие ложно, то вход в цикл не выполняется и управление передается оператору, следующему непосредственно за операторами тела цикла. Если же условие истинно, то происходит вход в цикл и однократное выполнение операторов. Как только достигнут конец тела цикла, управление передается на его заголовок, где снова вычисляется его условие.

Для того чтобы последовательность инструкций между begin и end была выполнена хотя бы один раз, необходимо, чтобы перед выполнением инструкции while условие было истинно;

Для того чтобы цикл завершился, необходимо чтобы последовательность инструкций между begin и end изменяла значения переменных, входящих в условие.

Вычислить сумму нечетных чисел от 1 до некоторого числа n program summa; uses crt; var n, s, i: integer; begin clrscr; s:=0; i:=1; writeln (‘Введите натуральное число n’); readln(n); while i<=n do begin s:=s+i; i:=i+2; end; writeln (‘сумма= ’,s); readln; end.

Составить таблицу значений функции 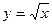на отрезке [2;4] с шагом 0,2. program func; uses crt; var x, y: real; begin clrscr; x:=2; while x<=4 do begin y:=sqrt(x); writeln (y:6:3); x:=x+0.2; end; readln; end.

Задачи цикл WHILE:

1) Вычислить сумму нечетных чисел от 1 до некоторого числа n

2) Составить таблицу значений функции 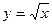на отрезке [2;4] с шагом 0,2.

3) Дано натуральное число. Определить:

а) количество цифр в нем;

б) сумму его цифр;

в) сумму m его последних цифр.

г) произведение его цифр;

д) среднее арифметическое его цифр;

е) сумму квадратов его цифр;

ж) его первую цифру;

4) Дано натуральное число.

а) Верно ли, что сумма его цифр больше 10?

б) Верно ли, что произведение его цифр меньше 50?

в) Верно ли, что количество его цифр есть четное число?

г) Верно ли, что это число четырехзначное?

5) Напечатать минимальное число, больше 200, которое нацело делится на 17.

6) Найти максимальное из натуральных чисел, не превышающих 5000, которое нацело делится на 39.

7) Дано натуральное число. Найти его наименьший делитель, отличный от 1.

8) Даны натуральные числа a и b. Найти НОД(a,b) и НОК(a,b).

9) Даны натуральные числа a и b, обозначающие соответственно числитель и знаменатель дроби. Сократить дробь, т.е. найти такие натуральные числа p и q, не имеющие общих делителей, что p/q=a/b.

10) Даны натуральные числа m и n. Получить все кратные им числа, не превышающие m*n. Условный оператор не использовать.

11) Дано натуральное число.

а) Получить число, получаемое при прочтении его цифр справа налево.

б) Приписать по двойке в начало и конец записи этого числа.

в) Удалить из него все цифры А.

г) Переставить его первую и последние цифры.

д) Приписать к нему такое же число. (получить это число)

12) Дано натуральное число. Определить номер цифры 3 в нем, считая от конца числа. Если такой цифры нет, ответом должно быть число 0, если таких цифр в числе несколько - должен быть определен номер самой правой из них.

13) Дан прямоугольник с размерами axb. От него отрезают квадраты максимального размера, пока это возможно. Затем от оставшегося прямоугольника вновь отрезают квадраты максимально возможного размера и т.д. На какие квадраты и в каком их количестве будет разрезан исходный прямоугольник?

14) Дана непустая последовательность целых чисел, оканчивающаяся нулем. Найти:

а) сумму всех чисел последовательности;

б) количество всех чисел последовательности.

15) Определить:

а) является ли заданное число степенью числа 3;

б) является ли заданное число степенью числа 5.

16) Дано число n.

а) Напечатать те натуральные числа, квадрат которых не превышает n.

б) Найти первое натуральное число, квадрат которого больше n.

Составное условие и вложенный условный оператор не использовать.

в) Верно ли, что его первая цифра не превышает 6?

г) Верно ли, что оно начинается и заканчивается одной и той же цифрой?

д) Определить, какая из его цифр больше: первая или последняя.

17) Дано натуральное число. Определить:

а) есть ли в нем цифра 3;

б) есть ли в нем цифры 2 и 5.

в) есть ли в нем цифра А.

г) верно ли, что в нем нет цифры В?

д) верно ли, что цифра А встречается в нем более К раз?

18) Дано натуральное число. Выяснить, является ли оно палиндромом ("перевертышем"), т.е. числом, десятичная запись которого читается одинаково слева направо и справа налево.

19) Найти все натуральные числа, меньшие 200, у которых сумма цифр равна 13.

20) Найти все целые числа от 30 до 350, у которых сумма цифр равна 15.

21) Найти все целые числа из промежутка от 1 до 100, у которых есть цифра ‘7’.

22) Найти все целые числа из промежутка от 50 до 150, у которых есть цифра ‘9’.

23) Найти все целые числа из промежутка от 10 до 200, у которых есть цифры ‘2’ и ’5’.

24) Найти размеры всех прямоугольников, площадь которых равна заданному натуральному числу s и стороны которого выражены натуральными числами. При этом решения, которые получаются перестановкой размеров сторон:

а) считать разными;

б) считать совпадающими.

Дата добавления: 2015-06-27