Системы продукций Поста (канонические системы)

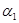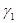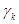
Каноническая система определяется собственным алфави­том А = { ,..., } (алфавитом констант), алфавитом X = {х₁,..., х_n} переменных, конечным множеством ак­сиом и конечным множеством правил вывода, имеющих вид , …, 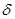и называемых продукциями (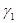, …, 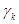), как обычно, называются посылками, 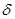— следствием). Ак­сиомы, а также посылки и следствия продукций — это слова в алфавите А U X; иначе говоря, они содержат кроме собственных букв системы еще и переменные. В даль­нейшем слова в алфавите A U X будем называть термами, а слова в A — просто словами. Переменные канонической системы аналогичны метапеременным в логических исчис­лениях; аксиомы канонической системы — это, по существу, схемы аксиом логических исчислений. Говоря о подста­новке в термы слов вместо переменных, мы всегда будем иметь в виду, что сохраняется обычное ограничение: вместо всех вхождений одной и той же переменной подставляется одно и то же слово (быть может, пустое).

Слово называется применением аксиомы , если получается подстановкой в слов вместо переменных. Слово непосредственно выводимо из слова 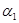,..., 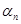при­менением продукции Р с n посылками, если найдется такая подстановка слов вместо переменных Р, которая посылки Р превратит в слова 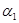,..., 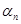а заключение Р — в слово . Например, слово bb непосредственно выводимо из слов acab, cabb применением продукции ах₁b, х₁bх₂ bх₂ при подстановке х₁ = са, х₂ = b. Последовательность слов на­зывается доказательством в канонической системе, если каждое слово этой последовательности — либо применение аксиомы, либо непосредственно выводимо из предыду­щих слов последовательности применением некоторой про­дукции системы. Слово называется доказуемым (или теоре­мой), если оно является последним словом некоторого доказательства.

Пример 6-7. а. Множество всех нечетных чисел в унар­ном представлении — это множество всех теорем канониче­ской системы с алфавитами {|}, {х}, аксиомой | и продукцией х х ||. Если эту продукцию заменить продукцией х хх, то получим каноническую систему, порождающую степени двойки (в унарном представлении): |, ||, |,...

б. Множество всех формул исчисления высказываний порождается канонической системой с алфавитами {a_l......, а_n, V, &, , , (,)}, {x_1, x₂}, аксиомами а₁,..., а_n и продукциями

x₁, x₂ (x₁ V x₂);

x₁, x₂ (x₁ & x₂); (6-15)

x₁, x₂ (x₁ x₂);

x₁ x_1.

Отметим, что здесь алфавит пропозициональных букв конечен. Для построения исчисления с бесконечным множе­ством пропозициональных букв сначала нужно построить формальную систему, порождающую это множество из конечного алфавита символов. Именно с этой целью в язы­ках программирования вводится индуктивное определение идентификатора; оно представляет собой формальную си­стему, порождающую бесконечное множество переменных языка из конечного алфавита букв и цифр.

При построении машин Тьюринга часто оказывалось удобным (а иногда необходимым) вводить вспомогательные символы, которые участвуют в процессе вычисления, но не присутствуют ни в исходных данных, ни в результа­те. Аналогичные средства вводятся и в формальных си­стемах.

Пусть дана каноническая система S с собственным алфа­витом А', в котором выделен подалфавит А. Если нас инте­ресуют только те теоремы S, которые являются словами в A, то будем говорить, что система S является канонической системой над А, А назовем основным алфавитом, А' — расширением А, а символы из A'\A— вспомогатель­ными.

Пример 6-8. а. Последовательность чисел 0, 1, 1, 2, 3, 5, 8..., в которой каждый член, начиная с третьего, ра­вен сумме двух предыдущих, называется последователь­ностью Фибоначчи, а ее элементы — числами Фибоначчи. Числа Фибоначчи в унарном представлении порождаются канонической системой над {|} со вспомогательным симво­лом *, аксиомой * l и двумя продукциями:

x_1* x₂ x₂*x₁x_2; x₁x₂ x₁.

В этой системе символ * служит маркером, разделяющим два числа, аксиома задает первые два числа последователь­ности (0 изображен пустым словом слева от маркера), пер­вая продукция из n-го и (n + 1)-го члена получает (n + + 1)-й и (n + 2)-й члены последовательности, вторая продукция из пары чисел выделяет первое; только приме­нение второй продукции дает слова в алфавите {|}.

б. Реализуем изложенный в примере 6-7б план построе­ния формул исчисления высказываний с бесконечным мно­жеством пропозициональных букв. Эти «буквы» будут обо­значаться символом а с числовым индексом, т. е. будут пред­ставлять собой слова вида a, a01, a523 и т. д., играющие роль идентификаторов (имен веременных). Система содержит основной алфавит А ={а, 0, 1,2,..., 9, V, &, , , (,)}, вспомогательные символы {i, f}, аксиому ai и l6 продукций:

х₁i x₁0i;

x₁i x₁li;

…………

x₁i x₁9i,

x₁i x₁f;

x₁f, x₂f (x₁ Vx₂)f;

x₁f, x₂f (x₁&x₂)f;

x₁f, x₂f (x₁ x₂)f;

x₁f x₁f;

x₁f x₁.

Первые десять продукций порождают идентификаторы; следующие пять продукций формализуют индуктивное опре­деление формулы (из этих пяти четыре последних отлича­ются от продукций (6-15) только символом f), последняя продукция служит для удаления символа f. Вспомогатель­ные символы играют здесь несколько непривычную роль — они, по существу, являются признаками (или метками) определенного класса слов: i — метка класса идентифика­торов, f — метка класса формул. Благодаря этому формаль­ный вид продукции очень близок к тексту соответствующей части индуктивного определения: 11-я продукция означает «всякий идентификатор есть формула», а 12-я: «если x₁ и x₂ — формулы, то (х₁Vx₂)— формула». Причем исполь­зования в формальных системах специальных символов как признаков классов широко используется в формальных системах Шмульяна, которые за недостатком места в данной книге не рассматриваются. Более подробно об использо­вании формальных систем такого рода для описания алго­ритмических языков говорится в [41], а о системах Шмуль­яна — в [53].

Связь канонических систем с системами подстановок довольно ясна, по крайней мере, в одну сторону; очевидно, что всякой подстановке 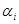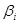соответствует продукция х₁ 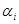x₂ = х₁ 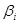x₂ поэтому для всякой системы подстановок легко построить эквивалентную ей каноническую систему. Соответствие в обратную сторону менее очевидно; однако о том, что оно существует, можно заключить, сопоставив теорему 6-14 (из которой следует, что множество теорем канонической системы перечислимо) с теоремой 6-15 (любое перечислимое множество можно представить как множе­ство заключительных слов в некоторой системе подстано­вок). Правда, понятие заключительного слова может пока­заться несколько искусственным и слишком уж приближаю­щим формальные системы к машинам Тьюринга; если рассма­тривать формальную систему как генератор элементов пере­числимого множества, более естественным было бы описа­ние перечислимого множества как множества теорем неко­торой формальной системы. Это нетрудно сделать, используя введенное ранее понятие канонической системы с расширен­ным алфавитом.

Теорема 6-18. Для любого перечисяимого множества М слов в алфавите А существует каноническая система над А, множество теорем которой совпадает с М.

Пусть М перечисляется машиной Тьюринга Т с алфави­том ленты А_т = {a₁,..., а_n}, первые m букв которого обра­зуют алфавит исходных данных (m 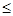n), множеством состо­яний Q = {q₁,..., q_z} и системой команд . Определим каноническую систему S над, А следующим образом: А = А_Т, А' =А_Т U Q_T; аксиома системы *; командам машины Т поставим в соответствие продукции аналогично тому, как это делалось при доказательстве теорем 6-15 и 6-16: например, команде q_ia_j q_ka_iR соответствует продук­ция x₁q_ia_jx₂ x₁a_iq_kx₂ [ср. (6-13)]. Кроме того, введем следующие m + 2 продукции:

x₁ * х₁а₁ *;

:

x₁* x₁a_m*;

x₁* q₁x₁;

q_zx₁ x₁.

Первые m продукций порождают из аксиомы все мно­жество слов в алфавите исходных данных с маркером в конце; (m + 1)-я продукция (стартовая) порождает из лю­бого исходного слова начальную конфигурацию; после этого работают продукции, соответствующие командам ма­шины Т; наконец, в заключительных конфигурациях (и только в них!) символ состояния выбрасывается и полу­чаются искомые теоремы в алфавите А. D

Итак, в терминах канонических систем можно описать любые перечислимые множества. Правда, используемое оп­ределение канонической системы (в частности, вид ее про­дукций) является слишком общим: применение продукции трудно назвать элементарным шагом (хотя свойство при­менимости продукции, как нетрудно видеть, разрешимо). Поэтому возникает задача нормализации канонических си­стем, т. е. придание им более простого, «нормального» вида.

Каноническая система называется нормальной, если она имеет одну аксиому, а все ее продукции имеют вид х x . Применение такой продукции к слову (если оно возможно) просто и стандартно: у слова вычеркивается начальный от­резок и к концу приписывается .

Теорема 6-19 (теорема Поста о нормальной форме). Для любой канонической системы CS с алфавитом А суще­ствует нормальная каноническая система NS над А, экви­валентная CS (т. е. множество теорем NS над А и множество теорем CS совпадают).

Прямое доказательство этой теоремы, содержащее метод построе­ния NS no CS, довольно сложно. Его можно найти, например, в [50], где оно занимает целую главу. Ограничимся косвенным доказатель­ством существования MS, а именно: покажем, что для любой системы подстановок S в алфавите А существует нормальная каноническая си­стема NS над А, эквивалентная S.

Пусть А = {a₁,..., а_n} и S содержит k подстановок 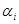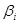. Опре­делим NS как систему с расширенным алфавитом А' = { a₁,..., а_n, ..., 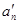} и k+ 2n продукциями:

a_ix x (i = 1,.... k); (6-16)

a_jx x ; (6-17)

a'_jx xa_j, (6-18)

где здесь и в дальнейшем обозначает слово 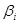, в котором все буквы из А заменены соответствующими буквами со штрихом.

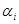
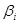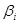
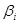
Пусть к слову в S применима подстановка : = _{1 i 2} и в S _{1 i 2}|— _{1 2} Но тогда в NS _{1 i 2}|— _{i 2 1}^||— _{2 1}^| |— ₁^| ₂^||— _{1 2}.Так как любой вывод |— 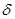в S есть цепочка подстановок, то по выводу |— 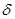в S можно построить вывод |— 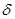в NS.

Пусть теперь в MS имеется вывод |— 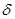, где , 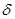— слова в А. Разобьем этот вывод на отрезки |— |— 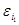|—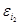…|— 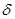, такие, что 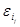и (для всех j) — слова в А, а все слова между ними содержат вспомогательные буквы, и рассмотрим для определенности первый из них |— 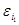. Если — слово в А, то продукциями (6-17), (6-18) из него можно получить лишь слова вида _{2 1}^|, ₂^| _1, ^|', где слова _{1, 2} таковы, что _{1 2} = . Так как 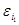— слово в А, то либо 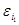= (но тогда этот отрезок из вывода можно удалить), либо на отрезке |— 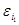была при­менена по крайней мере одна из продукций (6-16). Для любого вывода, содержащего между словами из А несколько применений продукций (6-16), в NS можно построить эквивалентный вывод, в котором между этими применениями вставлены слова из А. 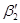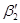Строгое доказательство этого утверждения опускаем; приведем лишь пример: выводу _{1 2}|— ₂ |— |— |— , в котором применены продукции ₁х x и ₂x x , соответствует вывод _{1 2}— ₂ |— ₂^||— ₂|— ₂ |— |— 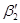, в котором они разделены словом ₂. Итак, можно считать, что в выводе |— 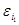продукция (6-16) — пусть это будет х x 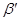—применена ровно один раз. Но тогда = _{1 2}, примене­нию продукции (6-16) предшествовало несколько (быть может, ни одного) применений (6-17) и место вывода, где применена продукция (6-16), имеет вид _{2 1}^| _{2 1}^| . Остаток _{2 1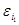}^| |— рассматриваемого отрезка не содержит применений (6-16), поэтому в силу свойств продукций (6-17), (6-18) 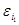= _{1 2}. Но тогда 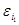получается из подстановкой , т. е. |— 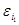в S. Индукцией до числу слов 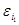доказываем, что |— 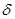в S. Отсюда следует эквивалентность S и NS, после чего о спра­ведливости теоремы нетрудно заключить из сопоставления теорем 6-15 и 6-18. D

В заключение раздела приведем без доказательства один результат об алгоритмической неразрешимости, который доказан Постом с помощью канонических систем и который часто используется для доказательства других неразреши­мостей (особенно в теории формальных грамматик).

Пусть дано конечное множество ( ₁, ),..., ( _m, ) пар слов в алфавите A. Поставим следующую проблему: существует ли последовательность i_l, i₂,..., i_N индексов, такая, что

… = … ?

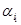
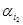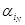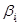
Эта проблема называется комбинаторной проблемой или проблемой соответствия Поста. Имеются два варианта ее формулировки: общая комбинаторная проблема Поста (для произвольного множества пар) и ограниченная комбинатор­ная проблема (для множества пар с фиксированной мощ­ностью m).

Теорема 6-20. Ограниченная комбинаторная проблема Поста для достаточно больших m алгоритмически неразре­шима. D

Отсюда следует неразрешимость и общей комбинаторной проблемы.

Формальные системы и алгоритмы. Итак, формальные системы оказываются столь же мощным средством для зада­ния конструктивных объектов, что и алгоритмы. С их по­мощью можно имитировать поведение машин Тьюринга, т. е. строить формальные системы, в некотором смысле ана­логичные алгоритмам. С другой стороны, понятие перечислимого множества в терминах формальных систем (опира­ющееся на теорему 6-18) выглядит более компактным, чем в терминах, скажем, машины Тьюринга. Поэтому возможны две концепции построения системы основных понятий, фор­мализующих идеи эффективности и конструктивности. Кон­цепция, описанная ранее и являющаяся исторически первой, кладет в основу понятие алгоритма. Вторая концепция, созданная Э. Постом ¹, опирается на понятия формальной (конкретнее, канонической) системы и перечислимого мно­жества, которое определяется просто как множество теорем формальной системы. Нормальную каноническую систему над алфавитом А можно представить как графе одной выде­ленной вершиной — аксиомой, остальные вершины кото­рого помечены словами в A — теоремами, ребра — это применения продукций, а пути из выделенной вершины в данную — возможные выводы данного слова. Множество слов в А, порождаемое системой, — это множество всех вершин графа, помеченных словами в А. Алгоритм — это формальная система особого, детерминированного вида, характеризующаяся тем, что в ней к каждой теореме при­менима не более чем одна продукция. Соответствующий граф представляет собой цепочку, изображающую вычи-

¹ Сжатое и блестяще написанное изложение этой концепции имеется в книге Мартин-Лефа в [48].

слительный процесс; аксиома в таком графе — это просто исходные данные алгоритма.

Другой способ детерминизации формальных систем — это фиксация порядка применения правил вывода. Напри­мер, нормальный алгоритм Маркова [47] — это упорядочен­ная система подстановок с двумя дополнительными согла­шениями: 1) i-я подстановка может быть применена, только если неприменимы 1,..., (i -1)-я подстановки; 2) если подстановка 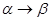применима к слову , то подставляется вместо самого левого вхождения в .

Основной акцент «алгоритмической» концепции — в ее детерминизме. Поэтому она естественна и удобна при опи­сании вычислительных процессов и устройств. Основной акцент «формально-системной» концепции — в компакт­ности конструктивного описания множеств. Примеры такого описания — формальные теории (§6-1 и 6-2). Другая группа примеров, крайне важных в прикладном отношении, — это алгоритмические языки программирования. Методы описа­ния языков и построения компиляторов для них опираются на теорию формальных грамматик, представляющих собой еще один вид абстрактных формальных систем. Основные понятия этой теории и ее приложения к языкам программи­рования изложены в [40, 41].

Дата добавления: 2015-06-27