Описание объекта управления

Задача 1

Реферат

Цель работы: систематизация, закрепление и расширение теоретических знаний, и получение практических навыков при расширении конкретных технических задач, развитие навыков самостоятельной работы с технической литературой в ходе расчета.

Объект исследования: в курсовой работе предлагается разработать алгоритмы изменения режима работы электрической схемы, содержащей ак­тивные и реактивные элементы, обеспечивающие минимизацию энергии ак­тивных потерь при переходе от одного режима работы схемы к дру­гому. Необходимо определить вид закона изменения ЭДС источника питания (управляющего воздействия) и проанализировать работу схемы при действии этой ЭДС.

Введение

На протяжении долгих лет очень эффективно используются математические методы моделирования и изучения жизни. Самые различные специалисты вынуждены прибегать к математическим методам оптимального управления. В связи с этим возникает множество проблем и трудностей, которые приходится решать.

Курсовая работа имеет своей целью систематизацию, закрепление и расширение теоретических знаний и практических навыков путем решения конкретных технических задач, развитие навыков само­стоятельной работы с литературой в ходе расчетов.

В процессе выполнения курсовой работы разрабатываются алгоритмы изменения режима работы электрической схемы, содержащей ак­тивные и реактивные элементы, которые обеспечивают минимизацию энергии ак­тивных потерь при переходе от одного режима работы схемы к дру­гому. Также определяется вид закона изменения ЭДС источника питания (управляющего воздействия) и анализируется работа схемы при действии этой ЭДС.

Оптимальное управление в RL-цепи

Математическая модель объекта получается на основе законов Кирхгофа:

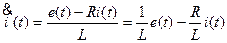
и имеет вид диф­ференциального уравнения

, (1)

где x(t)=i(t), u(t)=e(t),p, b – числа, равные p = – R/L, b = 1/L

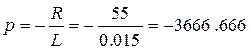
1.2. Конструирование функционала – критерия оптимальности.

Критерий оптимальности – квадратичный функционал



где - симметричная, неотрицательно-определенная матрица чисел, размерами ; - симметричная, положительно-определенная матрица чисел размерами .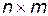

В данном случае вместо матриц используются числа, поэтому критерий оптимальности будет иметь другой вид:

, (2)

Это выражение представляет собой суммарную энергию активных потерь в схеме за время t₁–t_0.

Запишем выражение для активной мощности по­терь на сопротивлениях r и R:

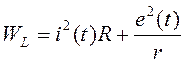или,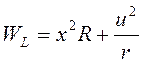

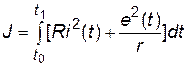
Таким образом, q = R=55, m = 1/r =1/5 =0,2, n = 0.

1.3. Формулировка задачи как вариационной задачи на услов­ный экстремум.

Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).

Таким образом, получаем следующую вариационную задачу:

Определить функции x(t) и u(t) доставляющие экстремум функционалу

,

при граничных условиях

,

и при дополнительном условии (уравнении связи)

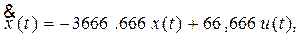
накладываемом на функции x(t), u(t), в классе которых ищется экстремум.

1.4. Синтез оптимального алгоритма управления.

1.4.1. Получение уравнений вариационной задачи.

Введем вспомогательную функцию (функцию Лагранжа)

,

где 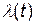- пока неизвестная функция, называемая неопределенным множителем Лагранжа.

Рассматриваемая задача называется задачей Лагранжа.

l(t) – неопределенный множитель Лагранжа, Φ – функция Лагранжа.

Запишем уравнения Эйлера для функции (они называются уравнениями Эйлера – Лагранжа)

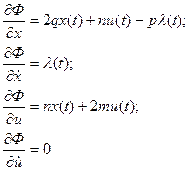
Решим совместно уравнения Эйлера – Лагранжа и уравнение связи. Это система трех уравнений для определения трех неизвестных x (t), u(t), l(t).

В итоге получаем систему уравнений

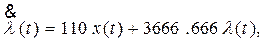(3)

(4)

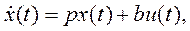
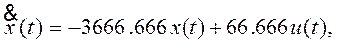(5)

Здесь (3), (4) – уравнения Эйлера – Лагранжа. К этим уравнениям добавлено уравнение объекта (5) (уравнение связи).

1.4.2. Отыскание решения уравнений вариационной задачи.

Уравнения (3) – (5) решаются в следующем порядке:

1) Выразим u(t) из (4):

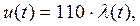
Затем подставим его в (5).

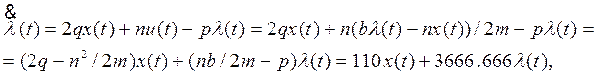
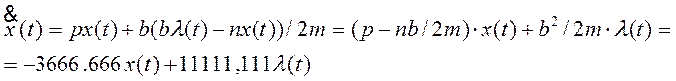
При этом получается система уравнений

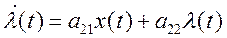, (6)

с коэффициентами

a₁₁ = p – nb/2m = - 3666.666,

a₁₂ = b²/2m = 11111.111,

a₂₁ = 2q – n²/2m =110,

a₂₂ = nb/2m – p = 3666.666.

Получим систему уравнений:

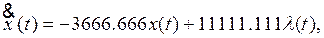
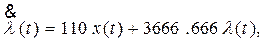
2) Запишем систему (6) в матричной форме

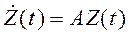, (7)

где

,

.

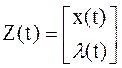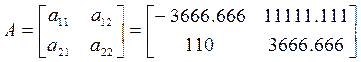3) Запишем решение уравнения (7) в соответствии с формулой Коши в виде:

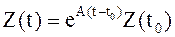, (8)

где

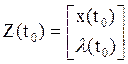– вектор начальных условий, а матричная экспонента определяется по формуле Лагранжа – Сильвестра

,

где l₁, l₂ – собственные числа матрицы А. Е - единичная матрица.

Найдем собственные числа матрицы А из условия . Получим:

,

,

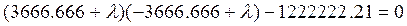Из системы следует, что для нахождения и необходимо знать начальные значения и .

(начальное положение объекта) задано, неизвестно.

Для определения неизвестного начального значения множителя Лагранжа l(t₀), входящего в (8) необходимо:

а) запишем (8) для момента времени t₁

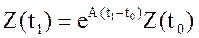
или

,

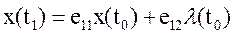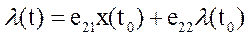, (9)

где e₁₁, е₁₂, е₂₁, е₂₂ – элементы матрицы (числа):

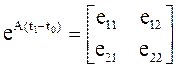
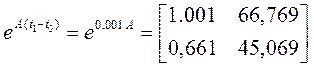
б) определим l(t₀) из первого уравнения системы (9)

Получили, что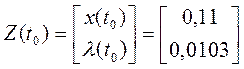

Решаем уравнение (7):

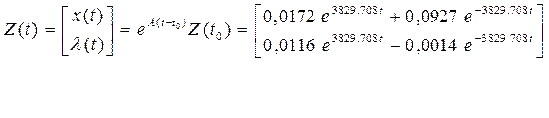
4) Решив уравнение (7), запишем выражения для оптимальной траектории и оптимального управления:

- оптимальная траектория

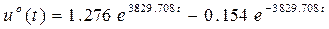- оптимальное управление

Дата добавления: 2015-06-27