Анализ процессов в системе. 1.5.1. Анализ процессов при оптимальном режиме

1.5.1. Анализ процессов при оптимальном режиме

Анализ процессов при оптимальном режиме построим графики x°(t), u°(t) на интервале tÎ[t₀,t₁]. Этот интервал разбивается на 10 частей и вычисляются значения x°(t) и u°(t) в этих точках.

t	x(t)	u(t)
	0,1099	1,122
0,0001	0,088432	1,766424
0,0002	0,080093	2,673106
0,0003	0,083646	3,976659
0,0004	0,099617	5,870618
0,0005	0,130379	8,636176
0,0006	0,180497	12,68393
0,0007	0,257414	18,61484
0,0008	0,372548	27,30946
0,0009	0,542994	40,05866
0,001	0,794057	58,75529

1.5.2. Анализ процессов при линейном изменении тока i(t)

Полагая, что ток изменяется линейно от заданного начального состояния до заданного конечного состояния

x_Л(t) = kt + d (i_Л(t) = kt + d),

(величины k, d найдем из условия прохождения i_Л(t) и u_Л(t) через заданные начальное и конечное значения)

x_Л(0) = d=0,11, x_Л(0.001) = 0.001k + 0,11 = 0,8

k=690

x_Л(t) = 690t + 0,11

запишем на основе (1)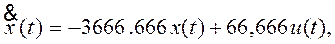

выражение для закона управления u_Л(t), обеспечивающее такое линейное изменение

.

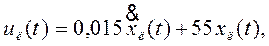
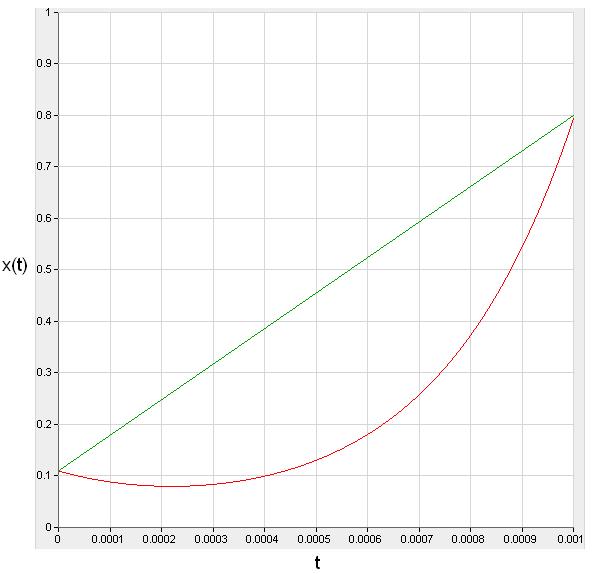
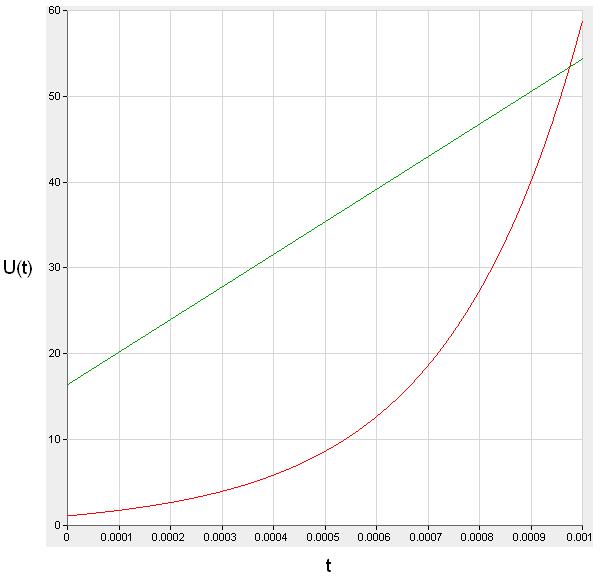
По полученным данным построим графики процессов x_Л(t), u_Л(t).

t	xл(t)	uл(t)
	0,11	16,4
0,0001	0,179	20,195
0,0002	0,248	23,99
0,0003	0,317	27,785
0,0004	0,386	31,58
0,0005	0,455	35,375
0,0006	0,524	39,17
0,0007	0,593	42,965
0,0008	0,662	46,76
0,0009	0,731	50,555
0,001	0,8	54,35

1.6. Сравнительная оценка процессов в схеме при оптимальном и линейном режимах.

1.6.1. Вычислим энергию активных потерь при оптимальном режиме, подставив в (2) x°(t) и u°(t).

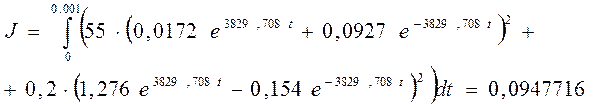
1.6.2. Вычислим энергию активных потерь при линейном режиме путем подстановки в (2) x_Л(t) и u_Л(t).

1.6.3. Сравнивая полученные величины, делаем вывод, что суммарная энергия активных потерь (затрачиваемая на нагрев) при линейном режиме больше, что говорит о целесообразности работы схемы в оптимальном режиме.

Задача 2

Для электрической схемы, содержащей источники ЭДС e(t) и источник тока J(t), активные сопротивления R₁, R₂, R₃, индуктивность L и емкость С

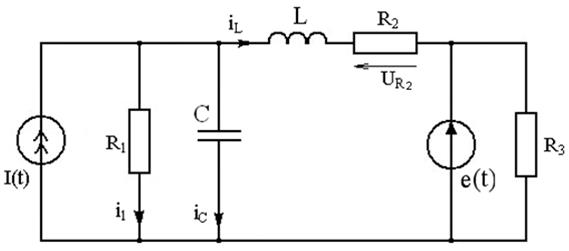
необходимо:

а) определить оптимальные законы изменения напряжения источника питания e⁰(t) и источника тока J⁰(t), приводящих к изменению тока через индуктивность L в схеме от заданного начального значения i_L0 до заданного конечного значения i_L1, и изменению напряжения на обкладках конденсатора С в схеме от заданного начального значения u_C0 до заданного конечного значения u_C1 так, чтобы суммарная энергия активных потерь (затрачиваемая на нагрев) при этом изменении была минимальной;

б) определить оптимальные законы изменения тока i⁰_L(t) и напряжения на обкладках конденсатора u⁰_C(t), соот­ветствующие оптимальным законам изменения e⁰(t), J⁰(t);

в) вычислить энергию активных потерь в схеме при оптималь­ном режиме изменения напряжений источников питания, тока и напряжения на обкладках конденсатора (e⁰(t), J⁰(t), i⁰_L(t), u⁰_C(t)) и сравнить ее с энергией активных потерь, затрачиваемой на нагрев при линейных изменениях тока i^Л_L(t) и напряжения на обкладках конденсатора u^Л_C(t) в схеме от начальных значений до конечных;

г) построить графики оптимальных и линейных изменений ЭДС, источника тока, тока и напряжения на обкладках конденсатора.

Значения параметров элементов схемы в зависимости от ва­рианта задания приведены в табл. 2.

Таблица 2

№ зад.	R1, Ом	R2, Ом	R3, Ом	L, Гн	С, мкФ	iL0, А	iL1, А	uC0, В	uC1, В
				0,015	3,5	0,11	0,8

Полагать t₀=0, t₁=10^-3 c.

Дата добавления: 2015-06-27