
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приведите и дайте краткую характеристику основных методов измерений
|
|
|
|
РЕШЕНИЕ
РЕШЕНИЕ
РЕШЕНИЕ
| № п/п | Содержание операции | Корреспонденция счетов | Сумма, руб. | |
| Дебет | Кредит | |||
| Выданы денежные средства под отчет из кассы | 161 300 | |||
| Списана в состав командировочных расходов сумма, указанная в счете гостиницы (без НДС) Учтен НДС, выделенный в счете гостиницы | 70 400 14 100 | |||
| Списана в состав командировочных расходов сумма суточных | 88 000 |
ЗАДАЧА
Организация приобрела право на использование технологии изготовления бумаги, стоимость которого составляет 2 017 800 руб., в том числе НДС по ставке 20%. По условию договора поставки предусмотрена форма расчета – предоплата в размере 100%.
У
Требуется: отразить на счетах бухгалтерского учета хозяйственные операции, связанные с приобретением нематериальных активов.
| № п/п | Содержание хозяйственной операции | Корреспонденция счетов | Сумма, руб. | |
| дебета | кредита | |||
| Перечислена предоплата за приобретаемые нематериальные активы с учетом НДС | 2 017 800 | |||
| Поступили нематериальные активы | 1 681 500 | |||
| Оприходованы нематериальные активы | 1 681 500 | |||
| Учтен НДС, выделенный поставщиком | 336 300 |
ЗАДАЧА
Требуется:
1. отразить на счетах хозяйственные операции и определить остаток денежных средств в кассе.
Исходные данные:
В организации остаток средств в кассе на 01.03 20__г. – 100 000 руб. В течение февраля произведены следующие хозяйственные операции:
| Дата | Содержание операции | Сумма, тыс. руб. | |
| 05.03 | С расчетного счета на основании чека № 44316 получены деньги и оприходованы в кассу | 924 000 | |
| 06.03 | По расходному кассовому ордеру выплачена ранее депонированная заработная плата | 671 750 | |
| 07.03 | По расходному кассовому ордеру №15 выдано завхозу на хозяйственные расходы | 111 900 |
| № | Дата | Содержание операции | Корреспондирующий счет | Сумма, тыс. руб. | |
| дебет | кредит | ||||
| 05.03 | С расчетного счета на основании чека № 44316 получены деньги и оприходованы в кассу | 924 000 | |||
| 06.03 | По расходному кассовому ордеру выплачена ранее депонированная заработная плата | 671 750 | |||
| 07.03 | По расходному кассовому ордеру №15 выдано завхозу на хозяйственные расходы | 111 900 |
Остаток денежных средств в кассе составит: 100000+924000-671750- 111900=240350 т.р.
2) Решите задачи:
Задача 1. Давление воздуха в заводской пневматической сети изменяется от 3 ат до 6 ат. Выразить давление в единицах системы СИ.
Задача 2. Определить приведенную погрешность амперметра, если его диапазон измерений от –5 А до +5 А, значение поверяемой отметки шкалы равно 3 А, а действительное значение измеряемой величины – 2,98 А.
Задача 3. Записать результат измерения следующих значений физических величин, пользуясь правилами округления: 6783,6 мм; 5499,74 с; 12,34501 кг. Погрешность ±0,0001.
Задача 4. По размерности обозначений величин определите, какие это физические величины и единицы их измерения:
1) L2MT - 2; 2) LT - 1; 3) LT - 2; 4) LMT - 2; 5) L2MT - 3.
Домашнее задание №2
Задача 5
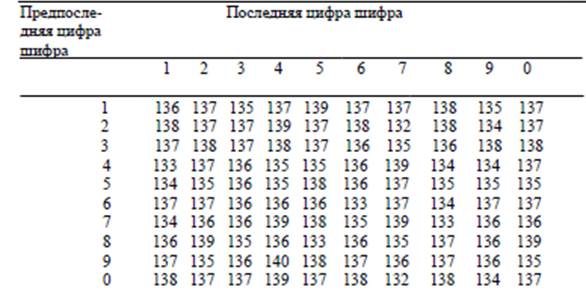
При многократном измерении одной и той же величины постоянного размера с равноточными значениями отсчета получены 50 независимых значений результата измерения (поправки внесены). Определить результат измерения.
Указания. Экспериментальные данные формируются из пяти серий (табл.2) по десять значений результата измерения в каждой (с первого по десятое).
Студент выбирает четыре серии по предпоследней цифре шифра (одна серия приведена в строке с соответствующим номером, три другие - в трех следующих строках), а пятую - по последней цифре шифра (столбец с соответствующим номером). Например, шифру 25-135 соответствуют серии, одна из которых приведена в строке 3, три другие - в строках 4, 5, 6, а пятая – в столбце 5; шифру 25-190 - серии в строках 9, 0, 1, 2 и
в столбце 0.
Таблица 2
Порядок расчета
Обработку экспериментальных данных (50 значений) следует осуществить по алгоритму, начиная с оценки среднего значения результата измерения. Обнаружение и исключение ошибок произвести по правилу трех сигм. Число значений результата измерения больше 40, поэтому дальнейший алгоритм обработки осуществить для условия 40...50. Проверку нормальности закона распределения вероятности результата измерения произвести по критерию К. Пирсона. При построении гистограммы учесть следующие рекомендации:
- интервалы, на которые разбивается ось абсцисс, следует выбирать по возможности одинаковыми;
- число интервалов выбирается в пределах 7...9;
- масштаб гистограммы назначается так, чтобы ее высота относилась к основанию примерно как 5/8.
Дальнейшую обработку провести в зависимости от результатов проверки нормальности закона распределения вероятности.
Указания.
1. Все экспериментальные данные собрать в единый массив в таблице.
| Qi | mi | Qi mi | Qi- 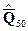
| (Qi- 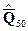 )2 )2
| mi (Qi - 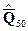 )2 )2
|
| - | ∑ | ∑ | - | - | ∑ |
2. В первую и вторую графы таблицы внести 50 независимых числовых значений результата измерения, каждое из которых повторилось m раз. Записать результат измерения.
3. Используя результаты вспомогательных вычислений, сведенные в третью графу таблицы, рассчитать оценку среднего арифметического значения результата измерения:

4. Выполнить вспомогательные расчеты, заполнив графы 2 и 3.
5. Используя вспомогательные вычисления в четвертой, пятой и шестой графах таблицы, рассчитать оценку стандартного отклонения результата измерения по формуле:
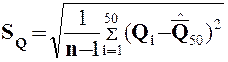
6. Проверить массив экспериментальных данных на наличие промахов по «правилу трех сигм».
7. Построить гистограмму. Выдвинуть гипотезу о законе распределения вероятности.
При использовании критерия К. Пирсона, вспомогательные расчеты выполняются по таблице:
| Интервалы | mi | ti | L(ti) | Pi | nPi | mi-nPi | 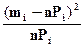
| |
| Qi-1 | Qi | |||||||
| (-∞ | ||||||||
| +∞ | ||||||||
| ∑ | ∑ | ∑ |
9.Определить, на сколько SQ отстоит от оценки среднего арифметического
значения 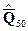 , правая граница Qi каждого интервала по формуле:
, правая граница Qi каждого интервала по формуле:
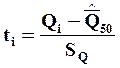 ;
;
10. По значению параметра ti можно определить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал 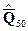 ± tiSQ.
± tiSQ.
Эта вероятность определяется интегралом вероятности – функцией Лапласа L(ti), представленной в приложении 1. Полученные значения L(ti) занесены в пятую графу таблицы.
11. Теоретическая вероятность Рi попадания в i -й интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, равна
Рi = L(ti )- L(ti-1).
Принимая во внимание, что L (-∞) = -0,5, а L (+∞) = +0,5, полученные значения Рi внести в соответствующую графу таблицы.
Суммирование результатов вспомогательных вычислений дает значение χ2 =….
12. При n>40...50 проверка гипотезы осуществляется по критерию К.Пирсона.
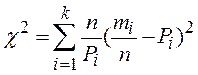
Если 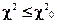 - гипотеза с выбранной вероятностью подтверждается, с вероятностью Р=… (приложение 2);
- гипотеза с выбранной вероятностью подтверждается, с вероятностью Р=… (приложение 2);
Если 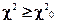 - с той же вероятностью гипотеза соответствия эмпирического закона теоретическому отвергается.
- с той же вероятностью гипотеза соответствия эмпирического закона теоретическому отвергается.
13. Рассчитать стандартное отклонение среднего арифметического значения результатов многократного измерения:
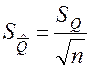
;
14. Из таблицы приложения 3 определяем параметр t при числе независимых измерений n ≥50 выбранной доверительной вероятности Р. Рассчитываем половину доверительного интервала, в котором находится результат измерения:
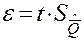
15. Определить пределы, в которых находится значение измеренной
величины: 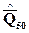 -
- 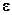 ≤ Q ≤
≤ Q ≤ 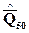 +
+ 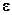 ;
;
Записать ответ:
С вероятностью P=…, результат измерения находится в доверительном интервале Q = […].
Задача 7
Выбрать ряды взаимосвязанных параметров А и В и определить порядковые номера членов этих рядов на основе следующих данных:
а) зависимость, определяющая связь параметров, имеет вид:
А = сBn,
где постоянный коэффициент с и показатель степени n определяются по последней цифре шифра студента из табл. 3;
б) параметр А задан рядом, определяемым из табл. 3 по предпоследней цифре шифра студента.
Таблица 3
| Параме-тры | Вариант | ||||||||||||||||||||||||||||
| Последняя цифра шифра | |||||||||||||||||||||||||||||
| c | 0,25 | 1,4 | 0,25 | 0,1 | |||||||||||||||||||||||||
| n | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | ||||||||||||||||||||||||
| Предпоследняя цифра шифра | |||||||||||||||||||||||||||||
| R10/2 | R5/3 | R40/3 | R20/3 | R10/3 | R5/2 | R40/2 | R20 | R10 | R5 | ||||||||||||||||||||
| (1,6...25) | ¯ | (2,8...8) | ¯ | (2...125) | ¯ | (1,25...2,5) | ¯ | (1,6...6,3) | ¯ | ||||||||||||||||||||
| (2,5...10000) | (1,4...11,2) | (1...250) | (2...4) | (1...16) | |||||||||||||||||||||||||
Результаты расчета свести в табл. по форме 1.
Указания. Задание 7 выполняется в следующей последовательности.
1. На основе системы предпочтительных чисел находим ряд параметров А и определяем его знаменатель jА (Приложение 4).
2. Находим приближенное значение параметра В1, соответствующее первому члену А1 ряда А.
3. Определяем знаменатель ряда В, находя значение jВ из соотношения
jА = jВ n.
4. Определяем ряд параметра В, его обозначение и порядковые номера членов ряда.
5. Результаты вносим в соответствующие графы формы 1.
Форма 1
___________________________________________________________________
Обозначение Обозначе- Знамена- Значение параметров
параметров ние ряда тель ряда ________________________________
1 2 3 4 5 6 7
___________________________________________________________________
________________________________
А Порядковые номера членов ряда
________________________________
___________________________________________________________________
________________________________
B Порядковые номера членов ряда
___________________________________________________________________
ПРИЛОЖЕНИЕ 1
Таблица значений функции Лапласа
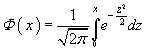
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,00000 | 0,50 | 0,19146 | 1,00 | 0,34134 | 1,50 | 0,43319 | 2,00 | 0,47725 | 3,00 | 0,49865 |
| 0,01 | 0,00399 | 0,51 | 0,19497 | 1,01 | 0,34375 | 1,51 | 0,43448 | 2,02 | 0,47831 | 3,05 | 0,49886 |
| 0,02 | 0,00798 | 0,52 | 0,19847 | 1,02 | 0,34614 | 1,52 | 0,43574 | 2,04 | 0,47932 | 3,10 | 0,49903 |
| 0,03 | 0,01197 | 0,53 | 0,20194 | 1,03 | 0,34849 | 1,53 | 0,43699 | 2,06 | 0,48030 | 3,15 | 0,49918 |
| 0,04 | 0,01595 | 0,54 | 0,20540 | 1,04 | 0,35083 | 1,54 | 0,43822 | 2,08 | 0,48124 | 3,20 | 0,49931 |
| 0,05 | 0,01994 | 0,55 | 0,20884 | 1,05 | 0,35314 | 1,55 | 0,43943 | 2,10 | 0,48214 | 3,25 | 0,49942 |
| 0,06 | 0,02392 | 0,56 | 0,21226 | 1,06 | 0,35543 | 1,56 | 0,44062 | 2,12 | 0,48300 | 3,30 | 0,49952 |
| 0,07 | 0,02790 | 0,57 | 0,21566 | 1,07 | 0,35769 | 1,57 | 0,44179 | 2,14 | 0,48382 | 3,35 | 0,49960 |
| 0,08 | 0,03188 | 0,58 | 0,21904 | 1,08 | 0,35993 | 1,58 | 0,44295 | 2,16 | 0,48461 | 3,40 | 0,49966 |
| 0,09 | 0,03586 | 0,59 | 0,22240 | 1,09 | 0,36214 | 1,59 | 0,44408 | 2,18 | 0,48537 | 3,45 | 0,49972 |
| 0,10 | 0,03983 | 0,60 | 0,22575 | 1,10 | 0,36433 | 1,60 | 0,44520 | 2,20 | 0,48610 | 3,50 | 0,49977 |
| 0,11 | 0,04380 | 0,61 | 0,22907 | 1,11 | 0,36650 | 1,61 | 0,44630 | 2,22 | 0,48679 | 3,55 | 0,49981 |
| 0,12 | 0,04776 | 0,62 | 0,23237 | 1,12 | 0,36864 | 1,62 | 0,44738 | 2,24 | 0,48745 | 3,60 | 0,49984 |
| 0,13 | 0,05172 | 0,63 | 0,23565 | 1,13 | 0,37076 | 1,63 | 0,44845 | 2,26 | 0,48809 | 3,65 | 0,49987 |
| 0,14 | 0,05567 | 0,64 | 0,23891 | 1,14 | 0,37286 | 1,64 | 0,44950 | 2,28 | 0,48870 | 3,70 | 0,49989 |
| 0,15 | 0,05962 | 0,65 | 0,24215 | 1,15 | 0,37493 | 1,65 | 0,45053 | 2,30 | 0,48928 | 3,75 | 0,49991 |
| 0,16 | 0,06356 | 0,66 | 0,24537 | 1,16 | 0,37698 | 1,66 | 0,45154 | 2,32 | 0,48983 | 3,80 | 0,49993 |
| 0,17 | 0,06749 | 0,67 | 0,24857 | 1,17 | 0,37900 | 1,67 | 0,45254 | 2,34 | 0,49036 | 3,85 | 0,49994 |
| 0,18 | 0,07142 | 0,68 | 0,25175 | 1,18 | 0,38100 | 1,68 | 0,45352 | 2,36 | 0,49086 | 3,90 | 0,49995 |
| 0,19 | 0,07535 | 0,69 | 0,25490 | 1,19 | 0,38298 | 1,69 | 0,45449 | 2,38 | 0,49134 | 3,95 | 0,49996 |
| 0,20 | 0,07926 | 0,70 | 0,25804 | 1,20 | 0,38493 | 1,70 | 0,45543 | 2,40 | 0,49180 | 4,00 | 0,49997 |
| 0,21 | 0,08317 | 0,71 | 0,26115 | 1,21 | 0,38686 | 1,71 | 0,45637 | 2,42 | 0,49224 | 4,05 | 0,49997 |
| 0,22 | 0,08706 | 0,72 | 0,26424 | 1,22 | 0,38877 | 1,72 | 0,45728 | 2,44 | 0,49266 | 4,10 | 0,49998 |
| 0,23 | 0,09095 | 0,73 | 0,26730 | 1,23 | 0,39065 | 1,73 | 0,45818 | 2,46 | 0,49305 | 4,15 | 0,49998 |
| 0,24 | 0,09483 | 0,74 | 0,27035 | 1,24 | 0,39251 | 1,74 | 0,45907 | 2,48 | 0,49343 | 4,20 | 0,49999 |
| 0,25 | 0,09871 | 0,75 | 0,27337 | 1,25 | 0,39435 | 1,75 | 0,45994 | 2,50 | 0,49379 | 4,25 | 0,49999 |
| 0,26 | 0,10257 | 0,76 | 0,27637 | 1,26 | 0,39617 | 1,76 | 0,46080 | 2,52 | 0,49413 | 4,30 | 0,49999 |
| 0,27 | 0,10642 | 0,77 | 0,27935 | 1,27 | 0,39796 | 1,77 | 0,46164 | 2,54 | 0,49446 | 4,35 | 0,49999 |
| 0,28 | 0,11026 | 0,78 | 0,28230 | 1,28 | 0,39973 | 1,78 | 0,46246 | 2,56 | 0,49477 | 4,40 | 0,49999 |
| 0,29 | 0,11409 | 0,79 | 0,28524 | 1,29 | 0,40147 | 1,79 | 0,46327 | 2,58 | 0,49506 | 4,45 | 0,50000 |
| 0,30 | 0,11791 | 0,80 | 0,28814 | 1,30 | 0,40320 | 1,80 | 0,46407 | 2,60 | 0,49534 | 4,50 | 0,50000 |
| 0,31 | 0,12172 | 0,81 | 0,29103 | 1,31 | 0,40490 | 1,81 | 0,46485 | 2,62 | 0,49560 | 4,55 | 0,50000 |
Продолжение таблицы значений функции Лапласа
| 0,32 | 0,12552 | 0,82 | 0,29389 | 1,32 | 0,40658 | 1,82 | 0,46562 | 2,64 | 0,49585 | 4,60 | 0,50000 |
| 0,33 | 0,12930 | 0,83 | 0,29673 | 1,33 | 0,40824 | 1,83 | 0,46638 | 2,66 | 0,49609 | 4,65 | 0,50000 |
| 0,34 | 0,13307 | 0,84 | 0,29955 | 1,34 | 0,40988 | 1,84 | 0,46712 | 2,68 | 0,49632 | 4,70 | 0,50000 |
| 0,35 | 0,13683 | 0,85 | 0,30234 | 1,35 | 0,41149 | 1,85 | 0,46784 | 2,70 | 0,49653 | 4,75 | 0,50000 |
| 0,36 | 0,14058 | 0,86 | 0,30511 | 1,36 | 0,41309 | 1,86 | 0,46856 | 2,72 | 0,49674 | 4,80 | 0,50000 |
| 0,37 | 0,14431 | 0,87 | 0,30785 | 1,37 | 0,41466 | 1,87 | 0,46926 | 2,74 | 0,49693 | 4,85 | 0,50000 |
| 0,38 | 0,14803 | 0,88 | 0,31057 | 1,38 | 0,41621 | 1,88 | 0,46995 | 2,76 | 0,49711 | 4,90 | 0,50000 |
| 0,39 | 0,15173 | 0,89 | 0,31327 | 1,39 | 0,41774 | 1,89 | 0,47062 | 2,78 | 0,49728 | 4,95 | 0,50000 |
| 0,40 | 0,15542 | 0,90 | 0,31594 | 1,40 | 0,41924 | 1,90 | 0,47128 | 2,80 | 0,49744 | 5,00 | 0,50000 |
| 0,41 | 0,15910 | 0,91 | 0,31859 | 1,41 | 0,42073 | 1,91 | 0,47193 | 2,82 | 0,49760 | ||
| 0,42 | 0,16276 | 0,92 | 0,32121 | 1,42 | 0,42220 | 1,92 | 0,47257 | 2,84 | 0,49774 | ||
| 0,43 | 0,16640 | 0,93 | 0,32381 | 1,43 | 0,42364 | 1,93 | 0,47320 | 2,86 | 0,49788 | ||
| 0,44 | 0,17003 | 0,94 | 0,32639 | 1,44 | 0,42507 | 1,94 | 0,47381 | 2,88 | 0,49801 | ||
| 0,45 | 0,17364 | 0,95 | 0,32894 | 1,45 | 0,42647 | 1,95 | 0,47441 | 2,90 | 0,49813 | ||
| 0,46 | 0,17724 | 0,96 | 0,33147 | 1,46 | 0,42785 | 1,96 | 0,47500 | 2,92 | 0,49825 | ||
| 0,47 | 0,18082 | 0,97 | 0,33398 | 1,47 | 0,42922 | 1,97 | 0,47558 | 2,94 | 0,49836 | ||
| 0,48 | 0,18439 | 0,98 | 0,33646 | 1,48 | 0,43056 | 1,98 | 0,47615 | 2,96 | 0,49846 | ||
| 0,49 | 0,18793 | 0,99 | 0,33891 | 1,49 | 0,43189 | 1,99 | 0,47670 | 2,98 | 0,49856 |
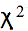 -распределение. Распределение Пирсона ПРИЛОЖЕНИЕ 2
-распределение. Распределение Пирсона ПРИЛОЖЕНИЕ 2
| m/α | 0,99 | 0,98 | 0,95 | 0,90 | 0,80 | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,001 |
| 0,00016 | 0,00063 | 0,00393 | 0,0158 | 0,0642 | 1,642 | 2,706 | 3,841 | 5,412 | 6,635 | 10,827 | |
| 0,0201 | 0,0404 | 0,103 | 0,211 | 0,446 | 3,219 | 4,605 | 5,991 | 7,824 | 9,210 | 13,815 | |
| 0,115 | 0,185 | 0,352 | 0,584 | 1,005 | 4,642 | 6,251 | 7,815 | 9,837 | 11,341 | 16,268 | |
| 0,297 | 0,429 | 0,711 | 1,064 | 1,649 | 5,989 | 7,779 | 9,488 | 11,668 | 13,277 | 18,465 | |
| 0,554 | 0,752 | 1,145 | 1,610 | 2,343 | 7,289 | 9,236 | 11,070 | 13,388 | 15,086 | 20,517 | |
| 0,872 | 1,134 | 1,635 | 2,204 | 3,070 | 8,558 | 10,645 | 12,592 | 15,033 | 16,812 | 22,457 | |
| 1,239 | 1,564 | 2,167 | 2,833 | 3,822 | 9,803 | 12,017 | 14,067 | 16,622 | 18,475 | 24,322 | |
| 1,646 | 2,032 | 2,733 | 3,490 | 4,594 | 11,030 | 13,362 | 15,507 | 18,679 | 20,090 | 26,125 | |
| 2,088 | 2,532 | 3,325 | 4,168 | 5,380 | 12,242 | 14,684 | 16,919 | 19,679 | 21,666 | 27,877 | |
| 2,588 | 3,059 | 3,940 | 4,865 | 6,179 | 13,442 | 15,987 | 18,307 | 21,161 | 23,209 | 29,588 | |
| 3,053 | 3,609 | 4,575 | 5,578 | 6,989 | 14,631 | 17,275 | 19,675 | 22,618 | 24,725 | 31,264 | |
| 3,571 | 4,178 | 5,226 | 6,304 | 7,807 | 15,812 | 18,549 | 21,026 | 24,054 | 26,217 | 32,909 | |
| 4,107 | 4,765 | 5,892 | 7,042 | 8,634 | 16,985 | 19,812 | 22,362 | 25,472 | 27,688 | 34,528 | |
| 4,660 | 5,368 | 6,571 | 7,790 | 9,467 | 18,151 | 21,064 | 23,685 | 26,873 | 29,141 | 36,123 | |
| 5,229 | 5,985 | 7,262 | 8,547 | 10,307 | 19,311 | 22,307 | 24,996 | 28,259 | 30,578 | 37,697 | |
| 5,812 | 6,614 | 7,962 | 9,312 | 11,152 | 20,465 | 23,542 | 26,296 | 29,633 | 32,000 | 39,252 | |
| 6,408 | 7,255 | 8,672 | 10,085 | 12,002 | 21,615 | 24,769 | 27,587 | 30,995 | 33,409 | 40,790 | |
| 7,015 | 7,906 | 9,390 | 10,865 | 12,857 | 22,760 | 25,989 | 28,869 | 32,346 | 34,805 | 42,312 | |
| 7,633 | 8,567 | 10,117 | 11,651 | 13,716 | 23,900 | 27,204 | 30,144 | 33,687 | 36,191 | 43,820 | |
| 8,260 | 9,237 | 10,851 | 12,443 | 14,578 | 25,038 | 28,412 | 31,410 | 35,020 | 37,566 | 45,315 | |
| 8,897 | 9,915 | 11,591 | 13,240 | 15,445 | 26,171 | 29,615 | 32,671 | 36,343 | 38,932 | 46,797 | |
| 9,542 | 10,600 | 12,338 | 14,041 | 16,314 | 27,301 | 30,813 | 33,924 | 37,659 | 40,289 | 48,268 | |
| 10,196 | 11,298 | 13,091 | 14,848 | 17,187 | 28,429 | 32,007 | 35,172 | 38,968 | 41,638 | 49,728 | |
| 10,856 | 11,992 | 13,848 | 15,659 | 18,062 | 29,553 | 33,196 | 36,415 | 40,270 | 42,980 | 51,179 | |
| 11,542 | 12,697 | 14,611 | 16,473 | 18,940 | 30,675 | 34,382 | 37,652 | 41,566 | 44,314 | 52,620 | |
| 12,198 | 13,409 | 15,379 | 17,292 | 19,820 | 31,795 | 35,563 | 38,885 | 42,856 | 45,642 | 54,052 | |
| 12,879 | 14,125 | 16,151 | 18,114 | 20,703 | 32,912 | 86,741 | 40,113 | 44,140 | 46,963 | 55,476 | |
| 13,565 | 14,847 | 16,928 | 18,939 | 21,588 | 34,027 | 37,916 | 41,337 | 45,419 | 48,278 | 56,893 | |
| 14,256 | 15,574 | 17,708 | 19,768 | 22,475 | 35,139 | 39,087 | 42,557 | 46,693 | 49,588 | 58,302 | |
| 14,953 | 16,306 | 18,493 | 20,599 | 23,364 | 36,250 | 40,256 | 43,773 | 47,962 | 50,892 | 59,703 |
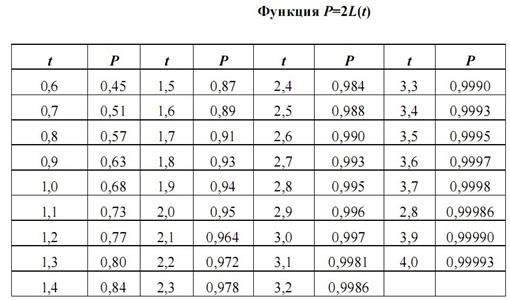
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 4
Основные ряды предпочтительных чисел в соответствии с ГОСТ 8032-84.
| Основные ряды | Номер предпочтительного числа | Мантиссы логарифмов | Расчетные величины чисел | Разность между числами основного ряда и расчетными величинами, % | |||
| R5 | R10 | R20 | R40 | ||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,0000 | |||
| 1,06 | 1,0593 | +0,07 | |||||
| 1,12 | 1,12 | 1,1220 | -0,18 | ||||
| 1,18 | 1,1885 | -0,71 | |||||
| 1,25 | 1,25 | 1,25 | 1,2589 | -0,71 | |||
| 1,32 | 1,3335 | -1,01 | |||||
| 1,40 | 1,40 | 1,4125 | -0,88 | ||||
| 1,50 | 1,4962 | +0,25 | |||||
| 1,60 | 1,60 | 1,60 | 1,60 | 1,5849 | +0,95 | ||
| 1,70 | 1,6788 | +1,26 | |||||
| 1,80 | 1,80 | 1,7783 | +1,22 | ||||
| 1,90 | 1,8836 | -0,87 | |||||
| 2,00 | 2,00 | 2,00 | 1,9953 | +0,24 | |||
| 2,12 | 2,1135 | +0,31 | |||||
| 2,24 | 2,24 | 2,2387 | +0,06 | ||||
| 2,36 | 2,3714 | -0,48 | |||||
| 2,50 | 2,50 | 2,50 | 2,50 | 2,5119 | -0,47 | ||
| 2,65 | 2,6607 | -0,40 | |||||
| 2,80 | 2,80 | 2,8184 | -0,65 | ||||
| 3,00 | 2,9854 | +0,49 | |||||
| 3,15 | 3,15 | 3,15 | 3,1623 | -0,39 | |||
| 3,35 | 3,3497 | +0,01 | |||||
| 3,55 | 3,55 | 3,5481 | +0,05 | ||||
| 3,75 | 3,7584 | -0,22 | |||||
| 4,00 | 4,00 | 4,00 | 4,00 | 3,9811 | +0,47 | ||
| 4,25 | 4,2170 | +0,78 | |||||
| 4,50 | 4,50 | 4,4668 | +0,74 | ||||
| 4,75 | 4,7315 | +0,39 | |||||
| 5,00 | 5,00 | 5,00 | 5,0119 | -0,24 | |||
| 5,30 | 5,3088 | -0,17 | |||||
| 5,60 | 5,60 | 5,6234 | -0,42 | ||||
| 6,00 | 5,9566 | +0,73 | |||||
| 6,30 | 6,30 | 6,30 | 6,30 | 6,3096 | -0,15 | ||
| 6,70 | 6,6834 | +0,25 | |||||
| 7,10 | 7,10 | 7,0795 | +0,29 | ||||
| 7,50 | 7,4989 | +0,01 | |||||
| 8,00 | 8,00 | 8,00 | 7,9433 | +0.71 | |||
| 8,50 | 8,4140 | +1,02 | |||||
| 9,00 | 9,00 | 9,9125 | +0,98 | ||||
| 9,50 | 9,4406 | +0,63 | |||||
| 10,00 | 10,00 | 10,00 | 10,00 | 10,000 |
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 996; Нарушение авторских прав?; Мы поможем в написании вашей работы!