N.V.Katargin, phd, docent, A.I.Bogomolov, phd, docent,V.I.Kostyunin, phd, docent

Research of the system consisting of manufacturers, power and criminals

Research of the system consisting of manufacturers of production, the crime appropriating a part of production, and the power which consumes production part is conducted, but reduces a crime. The system is described by the differential equations which are investigated by a method of final differences. The schedules describing dynamics of population and a crime depending on parameters of system are constructed.

Social and economic system, mathematical modeling.

Норвежский математик-экономист, лауреат Нобелевской премии Т.Хаавелмо (Trygve Magnus Haavelmo) изучал системы одновременных уравнений, описывающие экономические процессы. Он предложил систему из двух уравнений, описывающих развитие системы, включающей в себя N людей (население), производящих и потребляющих Y единиц продукции, причём Y отстаёт от N. Прирост населения пропорционален его количеству (модель Мальтуса), но при дефиците продукции происходит убыль населения.

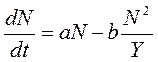
где N – население

Y – произведённая продукция

a, b, c, A – коэффициенты.

Нами проведено исследование данной системы уравнений методом конечных разностей в среде Excel. Начальное население N = 100, временной интервал dt = 0,01. Далее приведён пример: часть таблицы Excel с формулами и результатами расчетов.

Таблица 1.

	А	В	С
	N	dN	Y
			= A *A2^ c
	=А2+В3	=(a *A2- b *A2^2/C2)* dt	22,257
	71,967	-12,165	19,952
	62,432	-9,534	18,062
	54,818	-7,613	16,491

Некоторые результаты расчётов представлены в Таблице 2 и на Рисунке 1. Изменённые коэффициенты очерчены рамками. Номера графиков на Рисунке 1 соответствуют номерам колонок в Таблице 2.

Таблица 2.

№
a
b
c	0,7	0,7	0,7	0,7	0,7	0,7	0,6	0,5	0,5
A
Асимптота	0,6	60,8	333,6	33,1

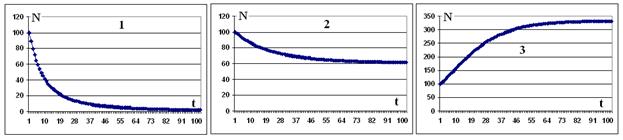
Рис. 1. Динамика популяции в зависимости от параметров системы.

На графиках видно, что решения системы уравнений близки к экспонентам, стремящимся к асимптотам, которые, как показали расчеты, не зависят от начального значения N.

Мы также исследовали расширенную модель Хаавельмо, включив в неё действующих лиц: криминал (К) и власть (V). Криминал забирает себе часть продукции Y, равную rK, размножается со скоростью fK и при дефиците продукции вымирает со скоростью sK ² /Y, т.е. по тому же закону, что и население. Власть уменьшает количество криминала с эффективностью е, т.е. на eV за временной интервал. Власть (точнее, расходы на власть) пропорциональна продукции (= vY) и уменьшает Y на величину V. Модель принимает вид:

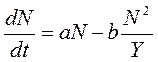
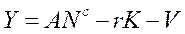
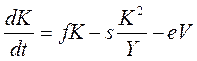
V = vY

Во всех расчетах использованы коэффициенты столбца 6 первой модели и одинаковые коэффициенты: размножения криминала f, убывания криминала s и пропорциональности продукции и власти v:

a	b	c	А	f	s	v
		0,7				0,1

Фрагмент таблицы Excel для расчётов представлен в Таблице 3, результаты расчётов – в Таблице 4 и на Рисунке 2.

Таблица 3.

	A	B	C	D	E
	N	dN	Y	K	V
			24,51		2,45
	121,45	21,45	25,68	3,19	2,56
	141,98	20,53	28,85	3,39	2,88

Таблица 4.

№	6 табл.2
r		0,2	0,33	0,2	0,2	0,2	0,1
e					15,6705	15,67051
Асимптота населения
Асимптота криминала		50,7					94,5

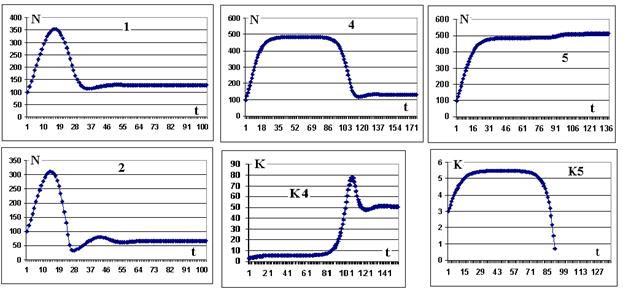
Рис. 1. Динамика популяции и криминала в зависимости от параметров системы.

Рассмотрение Таблицы 4 и Рисунка 2, а также эксперименты с начальными значениями N и K приводят к следующим выводам:

1. Население и криминал могут испытывать значительные колебания в начальной стадии процесса, но в конечном итоге стремятся к асимптотам, если не произошла катастрофа. Изменение начальных значений N и K не приводит к существенному изменению асимптот.

2. Криминал, присваивающий даже небольшую часть продукции, в перспективе резко сокращает население и производство: при r =10% асимптота населения падает в 3 раза (сравните № 6 таблиц 1 и 4), при r = 20% в 5 раз (№ 1). При r = 33% имеют место затухающие колебания населения и криминала, асимптота падает в 10 раз (№ 2); около 40% наступает катастрофа: население падает до нуля.

3. Эффективность власти е не влияет на асимптоты криминала и незначительно (до 15%) влияет на асимптоту населения, однако существуют критические значения коэффициентов e, при которых действия власти могут поддерживать количество населения довольно длительное время на высоком уровне (№ 4), но, в конечном итоге, криминал начинает быстро расти, затем и криминал, и население падают и стабилизируются (Рис.2, графики 4, К4). Критические значения е пропорциональны начальному значению криминала К (расчёты проведены при К₀ = 3, а при К₀ = 20 е_крит. = 92,5). При ничтожном превышении критического значения е (сравните № 4 и № 5) криминал через какое-то время полностью истребляется, население и производство стабилизируются на существенно более высоком уровне (Рис.2, № 5 и К5).

Представленная модель должна помочь изучению студентами основ экономико-математического моделирования, если эта дисциплина сохранится в российских вузах. Некорректно, но очень интересно проводить исследования модели при больших значениях коэффициента Мальтуса a (250-370). При этом возникают периодические биения, а потом непериодические, имитирующие динамический хаос, причём иногда в этом хаосе наступают периоды стабилизации населения и производства.

Катаргин Николай Викторович, к.ф.-м.н., доцент,

Тел. [phone]

e-mail nnnkkk@yandex/ru

Богомолов Александр Иванович, к.т.н., доцент,

Тел. [phone]

e-mail [e-mail]

В.И.Костюнин, к.т.н., доцент

Тел. [phone]

e-mail [e-mail]

Катаргин Богомолов Костюнин

Дата добавления: 2015-06-27