Метатеория исчисления высказываний

Исчисление высказываний, как синтаксическая теория, ставит своей задачей доказать все формулы, являющиеся теоремами исчисления высказываний. Но все это имеет смысл, если само исчисление высказываний является состоятельным, как синтаксическая теория, то есть положительно решены проблемы непротиворечивости, полноты, разрешимости, наличия связи с алгеброй высказываний и др. Решением подобного рода вопросов и занимается метатеория соответствующей синтаксической теории.

Определение 1. Синтаксическая теория, содержащая знак операции отрицания, называется непротиворечивой, если ни для какой формулы этой теории формулы и не могут одновременно быть теоремами этой теории.

В противном случае, теория называется противоречивой. Понятию же непротиворечивости можно дать и другое, эквивалентное первому определение.

Определение 2. Синтаксическая теория называется непротиворечивой, если существует формула, не являющаяся ее теоремой.

Покажем, что эти определения для исчисления высказываний эквивалентны. Пусть исчисление высказываний непротиворечиво по первому определению. Предположим противное, что исчисление высказываний противоречиво, в смысле второго определения. Тогда в нем доказуема любая формула, а, следовательно, и формула 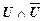. В силу правила 8 исчисления высказываний, получим, что

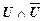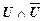ú- и ú- ,

т. е. как , так и были бы теоремами в этой теории, что противоречит условию. Следовательно, исчисление высказываний непротиворечиво в смысле второго определения.

Покажем, теперь обратное, что из непротиворечивости исчисления высказываний по второму определению следует его непротиворечивость в смысле первого определения. Если бы исчисление высказываний было противоречиво, в смысле первого определения, то в нем были бы доказуемы, например, формулы и . Тогда, по теореме эквивалентности из схемы аксиом 6 и свойства отношения эквивалентности 12 следует, что

ú- .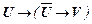

Применяя к последней формуле правило 6, получим

, ú- ,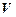

где 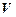- любая формула. Следовательно, исчисление высказываний противоречиво и во втором смысле.

Противоречивая синтаксическая теория никакой ценности не имеет, так как в ней выводимы любые формулы, и любая теорема одновременно и истинна, и ложна.

При доказательстве непротиворечивости исчисления высказываний мы будем использовать следующее утверждение.

Теорема 4.1. Всякая формула, являющаяся теоремой в исчислении высказываний, является ТИ-высказыванием в алгебре высказываний.

Непротиворечивость исчисления высказываний является непосредственным следствием этой теоремы. Действительно, в алгебре высказываний формулы и не могут быть одновременно ТИ-высказываниями. Следовательно, и одновременно не могут быть теоремами исчисления высказываний, что означает ее непротиворечивость.

Утверждение, обратное теореме 4.1, означает полноту исчисления высказываний относительно алгебры высказываний.

Теорема 4.2. В исчислении высказываний доказуема всякая формула, которая, как формула алгебры высказываний, является ТИ-высказываний.

По существу, эта теорема утверждает, что логических средств, т. е. аксиом и правил вывода, исчисления высказываний вполне достаточно для доказательства всех тождественно истинных формул алгебры высказываний.

Теоремы 4.1 и 4.2 формулируют необходимое и достаточное условия доказуемости формулы в исчислении высказываний.

Следствие 1. Для того чтобы формулы и 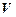были эквивалентны в исчислении высказываний, необходимо и достаточно, чтобы они были эквивалентны в алгебре высказываний.

Следствие 2. Формула 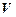выводима в исчислении высказываний из системы посылок 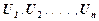, тогда и только тогда, когда она выводима из этой системы посылок в алгебре высказываний.

Таким образом, можно утверждать, что данные теории - алгебра высказываний и исчисление высказываний, являются адекватными, однако, они существенно отличаются по способу построения. Алгебра высказываний является семантической теорией, в ней все формулы понимаются содержательно, как функции на множестве 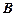. Исчисление высказываний, как мы уже говорили, является синтаксической теорией, в ней формулы – это определенные наборы символов, среди которых различаются лишь теоремы и не теоремы.

Кроме понятия полноты, названного относительной полнотой, существуют и другие понятия полноты.

Определение 3. Непротиворечивая синтаксическая теория называется полной, если из любых двух формул вида и , записанных на языке этой теории, одна является ее теоремой (или, как говорят, средств теории достаточно, чтобы доказать или опровергнуть любое утверждение, сформулированное на языке этой теории).

Определение 4. Непротиворечивая синтаксическая теория называется полной в узком смысле, если добавление к ее аксиомам любой недоказуемой в ней формулы приводит к противоречивой теории.

Из теоремы 4.1 следует, что исчисление высказываний неполно в смысле определения 3, так как в алгебре высказываний существуют формулы, не являющиеся ни тождественно истинными, ни тождественно ложными.

Теорема 4.3. Исчисление высказываний полно в узком смысле.

Из теоремы 4.3 следует, что выбор аксиом исчисления высказываний был сделан корректно.

Рассмотрим теперь вопрос о разрешимости исчисления высказываний. Синтаксическая теория называется разрешимой, если существует алгоритм, который для любой формулы позволяет сделать вывод, является ли она теоремой этой синтаксической теории.

Для того чтобы решить вопрос, доказуема ли в исчислении высказываний формула , достаточно определить (в силу теорем 4.1 и 4.2) является ли она ТИ-высказыванием алгебры высказываний.

Варианты заданий.

1. Доказать, что:

a) все аксиомы исчисления высказываний тождественно истинны;

b) все доказуемые в исчислении высказываний формулы тождественно истинны

2. Доказать теорему о полноте исчисления высказываний: всякая тождественно истинная формула доказуема в исчислении высказываний.

3. Доказать независимость схем аксиом исчисления высказываний.

4. Пусть L – исчисление высказываний со схемами аксиом Лукасевича.

a) Доказать, что все доказуемые в L формулы доказуемы в исчислении высказываний.

b) Доказать теорему дедукции для L.

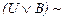
c) Положим , 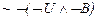. Доказать, что все доказуемые в исчислении высказываний формулы доказуемы в L.

Дата добавления: 2015-06-27