Переходим к следующему плану

Базисных клеток 7. План не вырожден.

Решаем задачу по методу максимального элемента.

Математическая модель двойственной задачи.

Составляем опорный план (табл. 2)

Табл.2

Bj Ai	П1	П2	П3	П4	П5	Ui
СО-1		3	^59 7	2	^11^–^W	^+^W	U1 =-1
	5		0
СО-2		^18 -W		^49	^32	^+^W 6		0	U2= 0
	2	3	4
СО-3		^29	^+W				^51	^-W	U3 =4
6	4	3	5	0
Vj	V1 =2	V2 =8	V3 =4	V4 =6	V5 = -4	W=11

Проверяем на вырожденность.

Z= m+n-1=3+5-1=7

Проверяем опорный план на оптимальность.

Задаем U₂ = 0 и определяем значения потенциалов.

Вычисляем оценки для всех незаполненных клеток (D_ij)

Опорное решение не является оптимальным, так как имеются отрицательные оценки.

Для клетки (1,5) с наименьшей оценкой (-5) строим цикл. Ставим в эту клетку коэффициент W со знаком «+» и применяя метод наибольшего элемента находим цикл, (табл. 2). Определяем из цикла W =11

Осуществляем сдвиг по циклу и строим следующий план (табл. 3)

.

Табл.3

Bj Ai	П1	П2	П3	П4	П5	Ui
СО-1		3	^59 7	2		^11	U1 =4
5	0
СО-2		^7 -W		^49	^43	^+W	U2= 0
	2	3	4	6		0
СО-3		^40	^+W				^40	^-W	U3 =4
6	4	3	5	0
Vj	V1 =2	V2 =3	V3 =4	V4 =6	V5 = -4

Проверяем план на оптимальность методом максимального элемента, как в п.З.

Задаем U₂ = 0 и определяем значения потенциалов.

Вычисляем оценки для всех незаполненных клеток (D_ij)

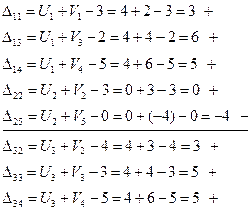
Определяем из цикла W=7

Осуществляем сдвиг по циклу и строим следующий план (табл. 4).

Табл. 4

Bj Ai	П1	П2	П3	П4	П5	Ui
СО-1		3	^59 7	2		^11	U1 =0
5	0
СО-2		2	3	^49 4	^43 6	^7 0	U2= 0
СО-3		^47 6	4	3	5	^33 0	U3 =0
Vj	V1 =6	V2 =7	V3 =4	V4 =6	V5 = 0

Проверяем план на оптимальность методом максимального

элемента, как в п.З.

Задаем U₂ = 0 и определяем значения потенциалов.

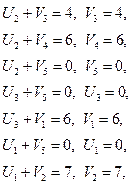
Вычисляем оценки для всех незаполненных клеток (D_ij)

план табл. 4 оптимален.

Определяем значение целевой функции прямойидвойственной задачи:

Исходя из первой теоремы двойственности в условии нашей задачи Z_max=Z_min=1149 (Z=Z’) последний план оптимален

Ответ:

1) Чтобы за рабочий день было убрано максимально возможное количество картофеля, следует распределить студентов по полям следующим образом:

– Из СО-1 выделить 59 человек для уборки картофеля на втором поле П₂, а 11 человек останутся в СО;

– из СО-2 выделить 49 человек для уборки картофеля на П_З и 43 человека для уборки картофеля на П₄, а 7 человек останутся в СО;

– из СО-3 выделить 47 человек для уборки картофеля на П₁, а 33 человека оставить в СО.

2) При данном оптимальном распределении студентов с четырех полей будет убрано 1149 центнеров картофеля.

Пример № 2

План перевозок:

Поставщики Аi	Потребители Вj:
	Запасы аi	Себестоимость	В1	В2	В3	В4
А1
А2
А3

Решение:

Проверяем на сбалансированность

Задача не сбалансированная. Введем фиктивного потребителя В₅ с потребностью в грузе, равной 200 ед. Стоимость перевозки для фиктивного потребителя определим равной нулю.

В качестве общей стоимости будем брать сумму затрат на доставку единицы продукции из соответствующего пункта и ее себестоимость в этом пункте.

Дата добавления: 2015-06-27