Твірна функція

Група

Вступ

У житті сучасного суспільства дуже важливу роль відіграє математика. Сьогодні математика знаходить широке застосування при вирішенні найрізноманітніших проблем науки. Однією з найважливіших областей сучасної математики є абстрактна алгебра, в центрі уваги якої знаходяться різні алгебраїчні структури, такі, як групи, підгрупи, напівгрупи, кільця тощо. Одним з фундаментальних розділів сучасної алгебри є теорія груп. Групи, по суті, є один з основних типів алгебраїчних структур. Знадобилася робота кількох поколінь математиків, що зайняла в цілому близько ста років, перш ніж ідея групи викристалізувалася з її сьогоднішньої ясністю.

Теорія груп почала формуватись в якості самостійного розділу математики наприкінці XVIII століття. Протягом перших десятиліть XIX століття вона розвивалася повільно і практично не привертала до себе уваги. Але потім, близько 1830 року, завдяки роботам Е.Галуа і Н.Абеля всього за кілька років вона зробила гігантський стрибок, який зробив глибокий вплив на розвиток всієї математики. З тих пір основні поняття теорії груп стали детально досліджуватися. В даний час теорія груп є однією з найбільш розвинених областей алгебри, що має численні застосування, в тому числі і у інших галузях математики.

Так, теорія груп використовується при розв'язуванні задач комбінаторного характеру. Ця робота і присвячена таким застосуванням теорії груп, зокрема в роботі розглядається відома комбінаторна задача про намиста з узагальненнями.

Найбільший внесок в розв’язанні даної задачі здійснив Вільям Бернсайд завдяки власному твердженню про кількість орбіт в підгрупі симетричної групи, яка зараз відома як лема Бернсайда. Хоча чимало сучасних дослідників схиляються до думки, що він не єдиний автор даної леми.

1. Хто все ж таки автор?

Вільям Бернсайд, англ. William Burnside, (1852-1927 рр.) англійський математик-алгебраїст. Член Лондонського Королівського товариства, професор Морського коледжу в Гринвічі. Відомий своїми працями з теорії груп, теорії представлень і характерів груп, вказав критерій розв`язності кінцевих груп. Йому належить також ряд робіт з теорії ймовірності, з аморфними функціями, з теорії хвиль в рідинах та інших.

Центральною частиною роботи Бернсайда була робота в області теорії представлень, де він міг розробити фундамент теорії, доповнюючи і інколи змагаючись з роботою Фробеніуса, який почав працювати в цій області в 1890-х роках. Одна із найвідоміших вкладів в теорію груп – це теорема Бернсайда про те, що кожна кінцева група, порядок яких ділиться менше ніж на три різних простих числа, розв’язна.

У 1897 році була опублікована класична робота Бернсайда «Теорія груп кінцевого порядку», де була опублікована славнозвісна лема. Друге видання (видане в 1911 році) стало стандартом в цій області на багото десятиліть. Головною відмінністю другого видання було включення в неї теорії характерів.

Бернсайд також відомий формулюванням проблеми, що носить його назву: «Чи буде конічною породжена група, в якій кожний елемент має кінчевий порядок, обов’язково кінцевий?».

Проте історики математики знайшли, що він був не перший, хто її відкрив світу: відомому французькому математику Огюстену Луї Коші в 1845 році була відома дана лема.

Огюстен Луї Коші фр. Augustin Louis Cauchy (21 серпня 1789 - 23 травня 1857) — французький математик, член Паризької академії наук (1816), Петербурзької академії наук (1831), Лондонського Королівського Товариства.

Автор 800 робіт з арифметики, теорії чисел, алгебри, математичного аналізу, диференціальних рівнянь, і т.д.

Особливо велике значення мають результати, отримані Коші: геометричне представлення комплексної змінної як точки, яка переміщається в площині тим чи іншим шляхом інтегрування (цю думку ще раніш висловили К. Гаус і ін.); вираження аналітичної функції у вигляді інтеграла (інтеграл Коші), та розклад функції в степеневий ряд; розробка теорії лишків і її застосування до різних питань аналізу.

Знайома була вона і Фердинанду Фробеніусу в 1887 році.

Фердина́нд Ге́орг Фробе́ніус нім. Ferdinand Georg Frobenius; (26 жовтня 1849 - 3 серпня 1917) — німецький математик-алгебраїст.

Основні роботи Фробеніуса стосуються теорії груп, зокрема, до теорії представлень.

Він першим довів, що асоціативне, дистрибутивне множення можливе тільки в просторах розмірності один (дійсні числа), два (комплексні числа) і чотири (кватерніони).

Напевно, лема була дуже відома, тому Бернсайд просто-на-просто опустив у своїй книзі імена авторів. У зв’язку з цим, в літературі можна зустріти інші назви цієї леми, наприклад, лема Коші-Фробеніуса або лема Коші-Фробеніус-Бернсайда.

Поняття множини є одним з найважливіших, фундаментальних понять сучасної математики. Це поняття є первісним. Вона не визначається, а роз’яснюється на конкретних прикладах. Так само як поняття точки і прямої в геометрії. Синонімами слова «множина» можна вважати такі слова, як сукупність, система, клас, збірка, тощо. Говорячи про множину, ми завжди будемо розуміти під цим поняттям певну сукупність деяких об’єктів, розглядаючи її як єдине ціле. Об’єкти, з яких складається множина, називаються елементами цієї множини.

Фундаментальним поняттям для леми Бернсайда є також поняття групи.

Означення 1. Множину 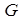називають групою, якщо справджуються такі висловлювання:

1. Задано закон множення (композиції), який впорядкованій парі елементів 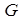ставить у відповідність добуток 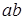— елемент 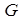, який називають добутком на a зліва або добутком a на справа.

2. Справджується сполучний закон множення: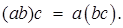

3. Існує ліва одиниця множення (нейтральний елемент) групи , тобто такий елемент групи, множення на який зліва не змінює жоден елемент групи: .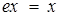

4. Для довільного елемента а групи існує лівий обернений до нього , тобто такий, при якому добуток оберненого елемента на сам елемент дорівнює лівій одиниці множення: .

Групу називають комутативною (абелевою), якщо множення комутативне, тобто добуток не залежить від порядку співмножників: .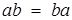

Закон асоціативності множення формулюють ще й так: добуток не зале- жить від порядку виконання дії множення (не плутати з порядком співмнож- ників). Саме у такій редакції його потрібно поширити на більшу кількість співмножників, розуміючи добуток як, наприклад, результат виконання дії множення у порядку запису зліва направо: . Множина взаємно однозначних відображень довільної множини в себе є групою щодо суперпозиції, тобто послідовного застосування відображень.

Теорема 1. Для довільної групи справджуються такі висловлювання.

1. Лівий обернений елемент є також правим оберненим елементом, який для кожного елемента групи єдиний: .

2. Ліва одиниця є також правою одиницею, тобто множення на неї справа не змінює жоден елемент групи: .

3. Одиниця множення у групі єдина.

Доведення.

Помножимо зліва рівність 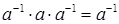на елемент, обернений до і використаємо асоціативність множення. В результаті отримаємо: , тобто лівий обернений елемент є також правим оберненим;

, тобто кожна ліва одиниця є одночасно правою одиницею; • помноживши зліва і справа довільний елемент a групи на його обернені і та по-різному розставляючи дужки, тобто використовуючи асоціативність множення, легко пересвідчитися, що обернений елемент єдиний: ;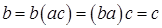

Обчислюючи добуток (одночасно лівих і правих) одиниць групи, легко пересвідчитися, що одиниця групи єдина: .

Означення 2. Введемо такі поняття:

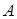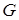1. Не порожню підмножину групи називають підгрупою групи 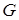, якщо:

Ø добуток двох елементів 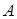також належить до ;

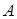Ø елемент, обернений до елемента з 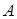також належить до .

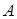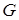2. Нехай — підгрупа групи . Правим класом групи 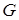за підгрупою 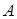називають множину вигляду де — довільний елемент групи G (аналогічно означають лівий клас суміжності).

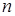3. Підстановкою (перестановкою) називають взаємно однозначне відображення скінченої множини у себе. Не обмежуючи загальності міркувань, надалі будемо розглядати лише множини вигляду — множини всіх перших натуральних чисел.

4. Транспозицією називають підстановку, яка кожному елементу, за виключенням двох, ставить у відповідність цей самий елемент.

5. Множину всіх підстановок на множині при сталому n називають симетричною групою і позначають .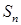

6. Порушенням порядку підстановки на множині {1, 2,..., n}, що числу ставить у відповідність число 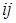при 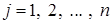, називають сумісну систему таких двох нерівностей: та .

7. Підстановку називають парною, якщо кількість транспозицій, у добуток яких можна розкласти дану підстановку, є парною.

8. Множину всіх парних підстановок на множині при сталому 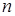називають знакозмінною групою і позначають .

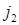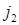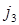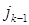9. Циклом довжини називають перестановку, яка певний елемент відображає у деякий елемент , — в 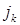,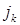..., — в , — в за умови, що всі елементи 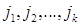— різні. Такий цикл позначають .

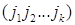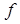10. Дві групи називають ізоморфними, якщо існує взаємно однозначне відображення f однієї групи в іншу, при якому образ добутку елементів однієї групи є добутком образів співмножників у тому самому порядку: . Таке відображення називають ізоморфізмом відповідних груп.

Зауваження 1. Істинними є такі твердження:

1. Транспозиція, що "міняє місцями" сусідні натуральні числа, змінює кількість порушень порядку на 1.

2. Довільна транспозиція змінює кількість порушень порядку на непарне число.

3. Парність кількості транспозицій у розкладі підстановки не залежить від конкретного подання добутком транспозицій і збігається з парністю кількості порушень порядку.

4. Цикл з непарної довжиною є добутком парної кількості транспозицій.

5. Цикл з парної довжиною є добутком непарної кількості транспозицій.

6. Підстановка є парною тоді й лише тоді, коли її подання добутком циклів без спільних елементів містить парну кількість циклів парної довжини.

Зауваження 2. Довільну підстановку можна подати добутком циклів без спільних елементів.

Зауваження 3. Для довільної скінченої групи множення справа (зліва) на певний елемент задає підстановку на множині елементів цієї групи. Тому довільна скінчена група ізоморфна підгрупі 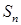, де — кількість елементів групи .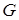

Зауваження 4. Класи суміжності за однією підгрупою мають однакову кількість елементів, що збігається з кількістю елементів підгрупи.

Означення 3. Твірною функцією послідовності 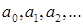називають степеневий ряд такого вигляду:

Надалі такі ряди будемо розглядати формально, тобто не досліджуючи питання збіжності, але використовуючи операції додавання, множення і (почленного) диференціювання твірних функцій. У задачах переліку числа 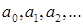— кількості об'єктів з певними властивостями. Тому твірну функцію називають рядом переліку.

Теорема 2. Якщо 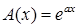при

то при натуральному довільному справджується така рівність:

Доведення.

тобто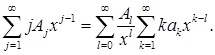

Коефіцієнти при лівої та правої частини цієї рівності відповідно дорівнюють звідки випливає формулювання теореми.

Дата добавления: 2015-06-27