Циклові індекси групи підстановок

Означення 4. Уведемо такі позначення й поняття.

1. Позначимо через 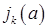кількість усіх циклів довжини , що входять у розклад підстановки a на цикли без спільних елементів. Тут лежить в межах від 1 до 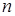— кількості об’єктів множини, на якій діє підстановка.

2. Характеристикою підстановки 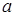називають впорядкований набір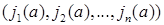

3. Цикловим індексом групи підстановок 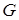на множині 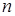елементів називають многочлен 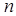змінних 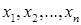такого вигляду:

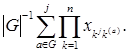
Такий многочлен позначають 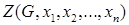або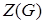

Зауваження 5. 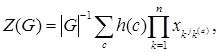де додавання здійснюють за всіма можливими характеристиками с елементів групи, 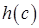— кількість елементів групи з характеристикою .

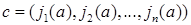Наприклад,

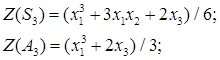
Теорема 3. При всіх натуральних справджуються такі рекурентні співвідношення:

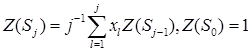
Доведення.

Для довільної підстановки 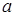позначимо через 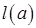довжину циклу, що містить -ий елемент. Маємо:

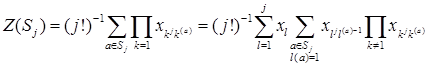
При сталому 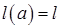доданки під знаком першої суми (при прогляданні виразу справа наліво — у порядку обчислення) в останньому виразі ті самі, що й для відповідної суми для 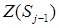. Кратність кожного такого доданка дорівнює кількості циклів довжини l, що містять -ий елемент. Згідно з комбінаторним правилом множення таку кількість можна подати добутком:

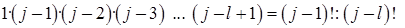
Врахувавши множник перед знаком другої суми, отримаємо твердження теореми.

Теорема 4.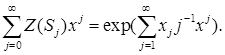

Доведення.

Див. твердження попередньої теореми й доведення теореми 2.

Дата добавления: 2015-06-27