Связь между корреляционными функциями и спектрами сигналов

Взаимная корреляционная функция

Если КФ показывает степень сходства между сдвинутыми копиями одного и того же сигнала, то взаимная корреляционная функция (ВКФ) позволяет измерить аналогичную величину для сдвинутых экземпляров двух разных сигналов:

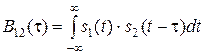
Свойства ВКФ несколько отличаются от свойств КФ:

1. , где и 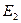- энергии сигналов и .

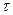2. , т.е. изменение знака равносильно взаимной перестановке сигналов.

3. Значение ВКФ при ничем не выделяется; максимум может быть расположен в любом месте оси .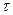

4. С ростом абсолютного значения 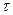ВКФ сигналов с конечной энергией затухает:

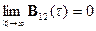
5. Если сигналы и не содержат особенностей в виде дельта-функций, их ВКФ не может иметь разрывов (т.е. обязана быть непрерывной функцией)

6. Если сигналы – напряжение, то размерность их ВКФ равна .

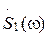Поскольку как корреляционные функции, так и спектры являются интегральными преобразованиями анализируемых сигналов, логично предположить, что эти характеристики как-то связаны друг с другом. Для выявления этой связи подвергнем взаимную корреляционную функцию преобразованию Фурье, считая, что сигналы и имеют спектральные функции и :

Полученный результат означает, что ВКФ связана преобразованием Фурье с так называемым взаимным спектром сигналов. Взаимный спектр 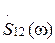для сигналов и представляет собой произведение их спектральных функций, одна из которых подвергнута комплексному сопряжению:

Отсюда следует важный вывод: если спектры сигналов не перекрываются, то их взаимный спектр равен нулю на всех частотах, а значит, равна нулю и их ВКФ при любых временных сдвигах 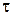. Таким образом, сигналы с не перекрывающимися спектрами являются некоррелированными.

Приняв = = ,получим аналогичный результат для КФ: она связана преобразованием Фурье с квадратом модуля спектральной функции, или с энергетическим спектром сигнала.

Отсюда следует еще один важный факт: КФ сигнала не зависит от его фазового спектра. Следовательно, сигналы, амплитудные спектры которых одинаковы, а фазовые различаются, будут иметь одинаковую КФ. Еще одно следствие заключается в том, что по КФ нельзя восстановить исходный сигнал (опять же из-за утраты информации о фазе).

Энергетические расчеты в спектральной области

ВКФ двух сигналов связана преобразованием Фурье с их взаимным спектром. Запишем эту связь в виде формулы обратного преобразования Фурье

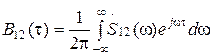
Теперь поставим в эту формулу значение и раскроем выражения для ВКФ и взаимного спектра. Получится соотношение, именуемое теоремой Рэлея:

Если теперь принять сигналы одинаковыми , получится соотношение, позволяющее вычислять энергию сигнала как во временной, так и в частной области и называемое равенством Парсеваля:

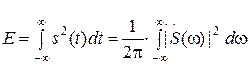
Для вычисления средней мощности периодического сигнала по коэффициентам его ряда Фурье запишем периодический сигнал s(t) в виде ряда Фурье в комплексной форме:

Применим к этому выражению формулу для расчета средней мощности за период:

Промежуток 0…Т соответствует целому числу периодов стоящей под интегралом комплексной экспоненты, поэтому интеграл будет равен нулю при всех . При экспонента становится константой, и интеграл будет равен Т:

В итоге, средняя мощность периодического сигнала равна сумме квадратов модулей коэффициентов его ряда Фурье.

Требования к работе:

по оформлению:

- курсовая работа должна быть оформлена в соответствии с требованиями, предъявляемым к текстовым документам (титульный лист, аннотация, содержание, текст работы, литература, приложения).

- шрифт Times New Roman, кегль 12 пт, одинарный междустрочный интервал, выравнивание текста – по ширине, нумерация страниц в нижнем колонтитуле;

- на титульном листе указывается: название курсовой работы, Фамилия И.О. исполнителя, факультет, специальность, курс, группа;

- список использованных источников - не менее 3-х, полное указание выходных данных для книжных и периодических изданий, адреса сайтов, с которых заимствован материал, по тексту реферата должны быть ссылки на источники;

по содержанию:

- работа должна содержать достоверные и актуальные сведения на достаточном научном уровне;

- работа, кроме текста, может дополнительно содержать: цветные иллюстрации, фрагменты программ, исполняемые модули и другие материалы, качественно дополняющие основную часть работы. Также работа может быть выполнена с использованием HTML, XML и т.д. Каждый компонент должен быть подписан (оформлен в виде рисунка) с указанием места привязки к тексту реферата;

по предъявлению:

- работа сдается не позднее, чем за 2 недели до зачета.

Преподаватель: д.т.н., профессор Галанина Наталия Андреевна

Дата добавления: 2015-06-27