Булева алгебра

Булевы алгебры – это частично упорядоченные множества специального вида.

Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.

Определение 1 (Булева функция). Булевой функцией от n аргументов x₁, x₂, …,x_n, называется функция f из n -ой степени множества {0, 1} в множество {0, 1} f: {0,1}ⁿ. → {0,1}, т.е. функция, которая произвольному набору из нулей и единиц ставит в соответствие значение функции f(δ₁,δ₂, …,δ_n) {0,1}.

Функции алгебры логики (ФАЛ) называются также булевыми функциями, двоичными функциями и переключательными функциями.

Булевой функцией описываются преобразования некоторым устройством входных сигналов в выходные. Пусть устройство f имеет n входов x₁, x₂, …,x_n на которые может подаваться (1) или не подаваться (0) ток и один выход, на котором ток есть (1) или (0). Таким образом, значение переменной x_i = 1 интерпретируется как поступление тока на i -й вход, а x_i = 0 - как не поступлении тока. Значение на выходе устройства f(δ₁,δ₂, …,δ_n) = 1, означает ток на выходе при заданном входе и f(δ₁,δ₂, …,δ_n) = 0 - тока на выходе нет.

Операции конъюнкции x 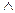y соответствует устройство с двумя входами и одним выходом. При этом значение выхода равно 1, тогда и только тогда, когда оба значения входов равны 1. Аналогично можно рассматривать и остальные операции.

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству {0, 1}. Множество {0, 1} мы будем в дальнейшем обозначать через B.

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B. При этом алгебра <B;W>, где W – множество всевозможных булевых функций, называется алгеброй логики.

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 ⁿ наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

Булева функция f(x₁, x₂, …,x_n) полностью определяется своей таблицей истинности

x1	x2	x3	…	xn-1	xn	f(x1, x2, …,xn)
			…			f(0, 0, … 0, 0)
			…			f(0, 0, … 0, 1)
. . .	. . .	. . .	… … …	. . .	. . .	. . .
			…			f(1, 1, … 1, 0)
			…			f(1, 1, … 1, 1)

В каждой строке таблицы истинности задается набор значений переменных (δ₁,δ₂, …,δ_n), а затем - значение функции на этом наборе.

Если булева функция f и формула φ имеют одну и ту же таблицу истинности, то формула φ представляет функцию f.

Определение:

Если в дистрибутивной решетке (S, ≤, ∧, ∨) для любого x∈S существует элемент ∈ S, такой, что

x ∨ = 0 (аксиома А6а),

x ∧ = 1 (аксиома А6б),

то элемент 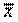называют дополнением, а решетку называют дистрибутивной решеткой с дополнениями или булевой алгеброй.

Дата добавления: 2015-06-27