Понятие формальной системы

Формальная система ( ФС ) считается заданной, если определены следующие ее компоненты: 1) алфавит; 2) совокупность правильно построенных формул; 3) множество аксиом; 4) множество правил вывода.

Алфавит ФС включает конечное или бесконечное число символов. Эти символы делятся на три группы – буквы, символы операций исвязок, вспомогательные символы (скобки различных видов, запятые и т.д.). Количество символов связок, символов операций и вспомогательных символов конечно, число букв может быть бесконечно за счет индексов, принимающих натуральные значения.

Любую конечную последовательность символов алфавита именуем формулой ФС. В совокупности формул ФС выделено множество правильно построенных формул ( ППФ ). Для ППФ задаютсяправила их конструирования и эффективная процедура, позволяющая по каждой формуле ФС определить, является ли она ППФ.

Множество аксиом – это выделенное подмножество ППФ. Если множество аксиом бесконечно, то предполагается наличие процедуры проверки по ППФ, является ли она аксиомой.

Правила вывода позволяют из имеющегося множества ППФ (утверждений) получать новые ППФ – непосредственные следствия этих утверждений.

Последовательность ППФ А ₁, А ₂,..., А _n называется выводом вФС, если для любого i= 1 ,…,n ППA А _i является либо аксиомой AС, либо непосредственным следствием некоторых ППФ множества (A ₁, A ₂, …, A _i-1), получаемым применением к этим ППФ некоторого правила вывода; ППФ A называется теоремой ФС, если в данной ФС имеется вывод, в котором последней ППФ является A.

Формальная система называется разрешимой, если существует алгоритм определения по произвольной ППФ, является ли она теоремой. Если такого алгоритме не существует, то рассматриваемая ФС именуется неразрешимой.

Правильно построенная формула B выводима из совокупностиППФ (А ₁, А ₂,..., А _n), если существует последовательность ППФ В ₁, В ₂,..., В _k такая, что В _k= В и для любого i= 1 ,..,k формула В _i является либо аксиомой ФС, либо формулой множества (А ₁, А ₂,..., А _n), либо непосредственным следствием некоторых ППФ множества (В ₁, В ₂,..., В _k), получаемых применением к этим ППФ одного из правил посылками или гипотезами. Формулы, выводимые из пустого множества посылок, являются теоремами.

Запись А ₁, А ₂,..., А _n |- В означает выводимость формулы В из множества посылок (А ₁, А ₂,..., А _n); запись |- В означает, что В является теоремой ФС. Если М ={ А ₁, А ₂,..., А _n}, то запись А ₁, А ₂,..., А _n |- В можно представить записью М |- В.

Очевидны следующие утверждения:

– если и , то ;

­– тогда и только тогда, когда в М имеется конечное подмножество M ₁ такое, что ;

– если и 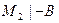для любой формулы В из множества M ₁, .

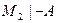Приведем простейший пример формальной системы. Считаем алфавит состоящим из символов |, =, +. Правила конструкции ППФ следующие:

1) | есть ППФ;

2) если а – ППФ, то а | также ППФ;

3) если а и b – ППФ, то а + b и а = b также ППФ;

4) других ППФ нет.

Система аксиом включает единственную аксиому: | = |. Единственное правило вывода следующее: из ППФ a = b выводится а + | = b |.

Очевидно, что теоремой в введенной ФС будет любая формула вида

|+|+|+…+|=|…|,

где слева и справа от знака = стоит одинаковое число символов |;

других теорем в ФС нет.

Дата добавления: 2015-06-27