
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип резолюции для логики высказываний
|
|
|
|
Легко проверяется, что формула
[(А  В)&(B
В)&(B 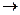 C)]
C)] 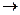 (A
(A  C) (1)
C) (1)
общезначима, т. е. является теоремой ИВ.
Лемма. Пусть в КНФ K(X 1, X 2 ,…,Xn) входят дизъюнкты D 1 и D 2 ,причем D 1 представим в виде D 1 '  Xi, а D 2 – в виде D 2 '
Xi, а D 2 – в виде D 2 ' 
 Xi. Тогда логическим следствием входящих в КНФ утверждений (дизъюнктов) является дизъюнкт D 1 '
Xi. Тогда логическим следствием входящих в КНФ утверждений (дизъюнктов) является дизъюнкт D 1 '  D 2 '.
D 2 '.
Действительно, дизъюнкт D 2 ' 
 Xi эквивалентен формуле Xi
Xi эквивалентен формуле Xi 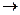 D 2'. В формулу (1) вместо A подставим D 1 ', вместо В - Xi и вместо С - D 2 '. Получаем следующую теорему ИВ:
D 2'. В формулу (1) вместо A подставим D 1 ', вместо В - Xi и вместо С - D 2 '. Получаем следующую теорему ИВ:
[(D 1 '  Xi)&(Xi
Xi)&(Xi 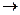 D 2 ')]
D 2 ')] 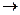 (D 1 '
(D 1 '  D 2 ').
D 2 ').
Так как утверждения D 1 '  Xi и Xi
Xi и Xi 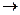 D2 ' входят в состав КНФ в качестве логического следствия образующих КНФ K(X1, X2,…,Xn) дизъюнктов, получаем D1'
D2 ' входят в состав КНФ в качестве логического следствия образующих КНФ K(X1, X2,…,Xn) дизъюнктов, получаем D1'  D2'. Лемма доказана.
D2'. Лемма доказана.
Формула D 1'  D 2' называется резольвентой формул D1= D1'
D 2' называется резольвентой формул D1= D1'  Xi и D2= D2'
Xi и D2= D2' 
 Xi . Резольвента D1'
Xi . Резольвента D1'  D 2' - логическое следствие дизъюнктов D 1 и D 2.
D 2' - логическое следствие дизъюнктов D 1 и D 2.
Резольвентой однолитерных дизъюнктов X и  X является противоречивая формула (пустой дизъюнкт) ÿ.
X является противоречивая формула (пустой дизъюнкт) ÿ.
Идея принципа резолюции заключается в проверке, выводим ли из дизъюнктов, составляющих КНФ K (X 1, X 2,…, Xn,), пустой дизъюнкт. Вывод конструируется последовательным построением резольвент. Выводимость из КНФ пустого дизъюнкта означает ее противоречивость.
Пример 3. Задана КНФ K (P,Q) = (Р  Q) & (
Q) & ( Р
Р  Q) & (Р
Q) & (Р 
 Q) & (
Q) & ( Р
Р 
 Q). Требуется доказать ее противоречивость,
Q). Требуется доказать ее противоречивость,
В состав рассматриваемой КНФ входят четыре дизъюнкта:
1) Р  Q;
Q;
2)  Р
Р  Q;
Q;
3) Р 
 Q;
Q;
4)  Р
Р 
 Q.
Q.
Строим следующие резольвенты (для каждой записываемой резольвенты в скобках указываются номера исходных для нее дизъюнктов):
5) Q (1,2);
6)  Q (3,4);
Q (3,4);
7) ÿ (5,6).
Из составляющих КНФ K (P,Q) дизъюнктов в качестве логического следствия выведенпустой дизъюнкт. Это означает противоречивость данной КНФ.
В дизъюнктах D 1'  Xi и D 2'
Xi и D 2' 
 Xi вхождения переменой Xi именуются контрарными. Так, в дизъюнктах 1) и 2), 3) и 4) контрарны вхождения буквы P;в дизъюнктах 5) и 6) контрарны вхождения буквы Q. Пустой дизъюнкт есть резолюция контрарных литер.
Xi вхождения переменой Xi именуются контрарными. Так, в дизъюнктах 1) и 2), 3) и 4) контрарны вхождения буквы P;в дизъюнктах 5) и 6) контрарны вхождения буквы Q. Пустой дизъюнкт есть резолюция контрарных литер.
Пример 4. Известно следующее: прямая L 1либо параллельна прямой L 2, либо совпадает с ней; параллельные прямые не имеют общих точек; прямые L 1 и L 2 имеют общую точку. Методом резолюции требуется доказать, что прямые L 1 и L 2 совпадают.
Исходные предположения на языке ИВ записываются следующим образом:
1) A  B;
B;
2) A 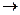
 C;
C;
3) C.
Требуется доказать справедливость утверждения B. Утверждение B является логическим следствием предположений 1),2),3) тогда и только тогда, когда формула
(A  B)&(A
B)&(A 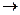
 C)& C &
C)& C &  B
B
невыполнима.
Так как формула A 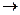
 C эквивалентна
C эквивалентна  A
A 
 C, нам требуется показать противоречивость следующей совокупности дизъюнктов:
C, нам требуется показать противоречивость следующей совокупности дизъюнктов:
1') A  B;
B;
2')  A
A 
 C;
C;
3') C;
4')  B.
B.
Конструируем резольвенты:
5') A (1', 4');
6')  C (5', 2');
C (5', 2');
7') ÿ (3', 6').
Итак, прямые L 1 и L 2 действительно совпадают.
Пример 5. Если футбольная команда A выигрывает, то город А ' торжествует; если команда В выигрывает, то торжествует город B '. Выигрывает либо команда A, либо команда В. Однако, если команда A выигрывает, то город В ' не торжествует; если выигрывает команда В, то город А ' не торжествует. Требуется доказать, что город А ' торжествует тогда и только тогда, когда не торжествует город В '.
Запишем посылки и заключения на языке ИВ:
1) A 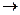 А';
А';
2) В 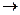 В';
В';
3) A  B;
B;
4) A 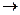
 В';
В';
5) В 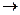
 А';
А';
6) (А'  В')&(
В')&( В'
В' 
 А').
А').
Отметим, что
 [(А'
[(А'  В')&(
В')&( В'
В' 
 А')]= (А '& В ')
А')]= (А '& В ')  (
( В'
В' 
 А')=
А')=
(А ' 
 В ')& (
В ')& ( А'
А'  В').
В').
Таким образом, требуется доказать противоречивость следующей совокупности дизъюнктов:
1)  A
A  А'; 2)
А'; 2)  В
В  В'; 3) A
В'; 3) A  B; 4)
B; 4)  A
A 
 В';
В';
5)  В
В 
 А'; 6) А'
А'; 6) А' 
 В'; 7) В'
В'; 7) В' 
 А'.
А'.
Конструируем резольвенты:
8) А'  В (1,3);
В (1,3);
9)  В
В  А' (2,6);
А' (2,6);
10) А' (8,9);
11) A 
 А' (3,5);
А' (3,5);
12)  A
A 
 А' (4,7);
А' (4,7);
13)  А ' (11,12);
А ' (11,12);
14) ÿ (10,13).
Решение закончено.
Теорема о полноте принципа резолюций. Если конечная совокупность дизъюнктов противоречива, то данный факт можно доказать, основываясь на принципе резолюции, т. е. путем последовательного конструирования резольвент, вплоть до получения пустого дизъюнкта.
Верхняя оценка временной вычислительной сложности, основанная на принципе резолюции алгоритма проверки противоречивости КНФ, экспоненциальна, что связано с NР— полнотой рассматриваемой проблемы.
При реализации данного алгоритма осуществляется поиск вывода пустого дизъюнкта. Некоторые направления поиска могут оказаться тупиковыми, полученные при этом результаты в найденном выводе пустого дизъюнкта не используются.
Так возникает вопрос о построении стратегий поиска, обеспечивающих в случае противоречивости рассматриваемой совокупности утверждений достаточно быстрый вывод пустого дизъюнкта (по оценке "в среднем").
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!