Первая итерация

Задание 1. Проектирование однослойной искусственной нейронной сети. Общие сведения.

Содержание пояснительной записки

Рекомендации по выполнению КР

Начинать работу следует с детального и внимательного изучения задания на КР и его анализа. После анализа задания студенту необходимо изучить настоящие методические указания и необходимые разделы рекомендуемых литературных источников, приведенных в указаниях.

Пояснительная записка к курсовой работе должна содержать

- титульный лист

- задание на проектирование;

- реферат;

- содержание;

- основная часть;

- перечень используемой литературы;

- необходимые приложения.

Основная часть состоит из разделов, связанных с одной из решаемых в работе задач. Каждый из разделов должен содержать постановку задачи, теоретическую, расчетную и графическую части. В теоретической части излагаются возможные методы решения задачи, обоснование выбранного подхода к ее решению и результаты решения, если для их получения не требуется проведения расчетов. Здесь же приводятся математические преобразования, необходимые для выполнения расчетной части. В расчетной части приводятся требуемые расчеты. Графическая часть содержит материал, иллюстрирующий результаты, полученные в разделе. Графический материал сопровождается необходимыми пояснениями. Каждый раздел заканчивается выводами.

6. Теоретическая часть

6.1 Понятие искусственной нейронной сети. Общие сведения

Искусственная нейронная сеть представляет собой совокупность взаимосвя-занных искусственных нейронных элементов, каждый из которых может быть представлен структурной схемой (рис. 1):

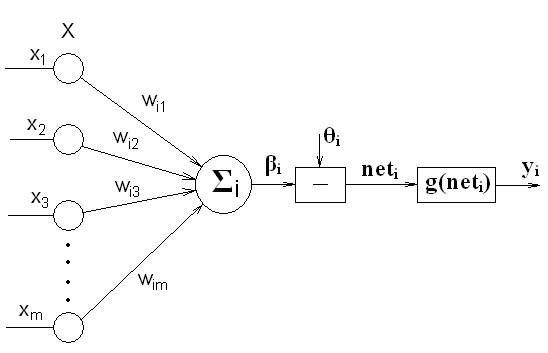
_{Рис. 1}

где Х – входной векторный сигнал ИНС;

х_j – j – тая компонента входного векторного сигнала ИНС;

w_ij – вес связи i – того нейронного элемента с j – тым входом ИНС;

Σ_i – сумматор i - того нейронного элемента;

β_i – результирующий сигнал на выходе сумматора i - того нейронного элемента;

θ_i – некоторый пороговый уровень.

В соответствии с этим рисунком модель формального нейрона может быть описана функцией вида

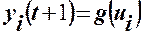, (1)

где y_i(t+1) – реакция i-того нейрона на входное воздействие;

g(•) – функция преобразования;

u_i – сетевая функция, определяемая в случае ее линейности выражением

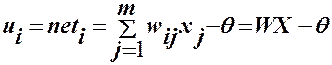(2)

Структура нейронной сети отображается направленным графом, в котором вершины - это НЭ, а дуги представляют связи между НЭ. Дуга, направленная от НЭ с номером j к НЭ элементу с номером i, характеризуется весом w_ij.

Выделяют следующие основные разновидности структур ИНС: однослойные ИНС с прямыми связями (рис. 2):

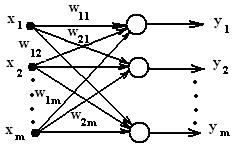
Рис. 2

многослойные ИНС с прямыми связями (рис. 3):

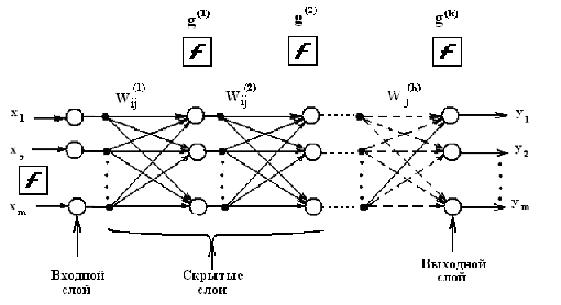
Рис. 3

однослойные рекуррентные ИНС (ИНС с обратными связями) (рис. 4):

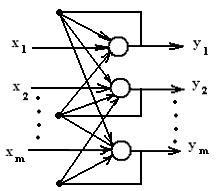
Рис.4

многослойные рекуррентные ИНС (рис. 5):

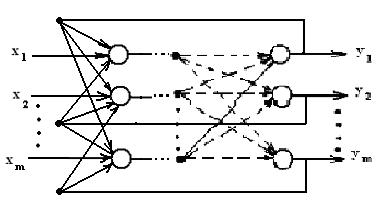
Рис. 5

Для решения простых задач распознавания как правило используют однослойные или многослойные сети с прямыми связями.

Связи входов сети с соответствующими НЭ могут быть заданы матрицей весов связей W

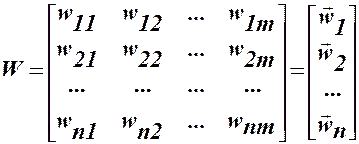, (3)

где 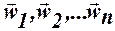- векторы весов НЭ с номерами 1,2,... n.Если между некоторым входом и НЭ нет связи, то соответствующий вес равен нулю.

В многослойной сети с прямыми связями выходы одного слоя НЭ выступают в роли входов другого слоя НЭ. Внутренние слои многослойной ИНС называют скрытыми слоями. Реакция i-го выходного НЭ многослойной ИНС вычисляется последовательным применением выражения (1). Например, если сеть является двухслойной, то

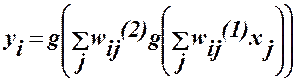(4)

Поведение рекуррентных ИНС сложнее из-за наличия обратных связей.

Таким образом, выполнить проектирование ИНС сводится к выбору ее структуры, определению в общем случае матриц весовых коэффициентов W для каждого слоя ИНС, определению θ_i, а также функции преобразования.

В качестве функции преобразования в ИНС применяются следующие основные функции:

- ступенчатая функция (функция Хевисайда)

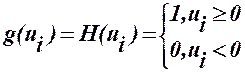(5)

- линейная функция с насыщением

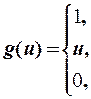
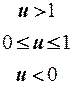(6)

- знаковая функция

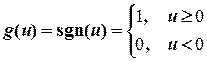(7)

- униполярная сигмовидная функция

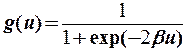, (8)

- биполярная сигмовидная функция, представляющая собой гиперболический тангенс

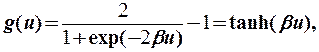(9)

- гауссова функция

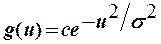(10)

где σ, с - постоянные коэффициенты.

В ИНС наиболее часто используется два типа НЭ:
- НЭ с линейной сетевой функцией вида (2) и функцией преобразова-ния вида (5) или (7). Такие НЭ называются линейными пороговыми элемен-тами (ЛПЭ). Сигналы, распространяющиеся в сетях, составленных из ЛПЭ, являются бинарными и принимают значения 0 или 1, либо +1 и -1.

- НЭ с линейной сетевой функцией (2) и функцией преобразования
вида (8) или (9). Такие НЭ называются линейно-непрерывными элементами (ЛНЭ). Сигналы, распространяющие в сетях из ЛНЭ, принимают произволь-ные значения из диапазона [0,1] или [-1,1].

По своей выходной реакции на входной сигнал сети можно разделить на сети, вырабатывающие признак входного воздействия и сети, восстанав-ливающие входное воздействие или ассоциированный с входным воздейст-вием сигнал. Сети, вырабатывающие на своём выходе признак входного сигнала, как правило, имеют столько выходов, а соответственно и нейронов, сколько входных полезных сигналов может присутствовать на их входах.

Вообще говоря, для разделения множества входных образов, например, по двум классам достаточно всего одного выхода. При этом каждый логический уровень – "1" и "0" – будет обозначать отдельный класс. На двух выходах можно закодировать уже 4 класса и так далее. Однако результаты работы сети, организованной таким образом, не очень надежны. Поэтому для повышения достоверности классификации желательно ввести избыточ-ность путем выделения каждому классу одного нейрона в выходном слое.

Число выходов сетей, предназначенные для восстановления входного сигнала или ассоциированного с ним сигнала соответствует размерности выходного сигнала.

Число входов cети определяется размерностью входного вектора.

6.2.1.Простой персептрон. Обучение простого персептрона.

НЭ, описываемый функцией

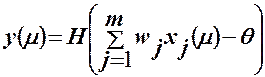(11)

где Н(•) - единичная ступенчатая функция Хевисайда, называется простым персептроном.

В качестве функции преобразования персептрона может использо­ваться также знаковая функция sgn(•). В этом случае входные и выходные сигналы персептрона будут биполярными.

Задача обучения персептрона заключается в поиске такого вектора весов w= (w,,w₂,...,w_m) и порогового значения θ, при которых будет обеспечиваться совпадение желаемой 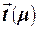и действительной реакции персептрона 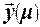на заданный входной вектор 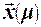. Если

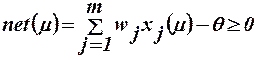, (12)

то выходной сигнал НЭ в силу использования в качестве функции преобразо-вания функции Хевисайда будет равен +1. Это означает, что входной вектор 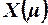принадлежит классу, на который настроен НЭ. В ином случае входной вектор не принадлежит этому классу. При этом сетевая функция НЭ

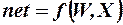
играет роль дискриминантной функций, позволяющей установить принад-лежность вектора 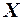классу.

Идея обучения персептрона состоит в следующем. На вход персеп­трона подаются последовательно входные векторы 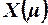. Одновременно с этим выходная реакция персептрона 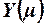сравнивается с желаемой реак­цией 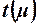. Если указанные реакции совпадают, то никаких действий не предпри-нимают. Если 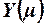≠ 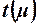, то вектор весов персептрона 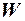изме­няется на величину 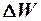. Адаптация весов выполняется с помощью правила

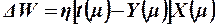(13)

где η - коэффициент обучения, η > 0. Если обозначить ошибку обучения через 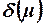, т.е. 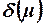= 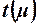- 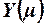, то правило обучения можно переписать в виде

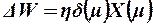(14)

Таким образом, если 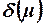=0, то вектор весов не меняется. Если 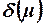>0, то вектор весов 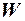меняется в направлении вектора .

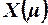Для простого персептрона в силу того, что в качестве функции преобразования используется функция Хевисайда, значение 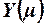может принимать только значения +1 (если на входе нейрона присутствует сигнал, на который “настроен” нейрон) или 0 (если сигнал на входе не соответствует сигналу настройки). Очевидно, что и желаемое значение реакции нейрона 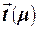будет равно +1, если на входе нейрона присутствует сигнал, на который “настроен” нейрон, и 0 в противном случае. Значение же выходной реакции нейрона будет зависеть от значения и знака аргумента функции преобразо-вания (функции Хевисайда), то есть от значения величины сетевой функции 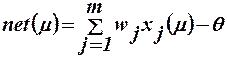. В соответствии с этим реакция нейрона на входное воздействие будет полностью определяться значением сетевой функ-цией. Поэтому в качестве желаемой реакции можно принять желаемое зна-чение сетевой функции, которое при входном сигнале, на который “настро-ен” нейрон на входной сигнал будет больше или равно 0, то есть

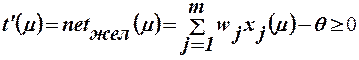. (15)

Если добавить к обеим частям неравенства θ, выражение (15) преобра-зуется к виду

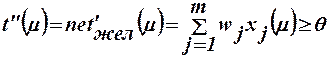. (16)

Полученное выражение показывает, что при данном подходе к опреде-лению значения желаемой реакции её значение должно быть больше θ, то есть .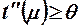

С учетом этого адаптация весов выполняется с помощью правила

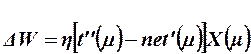(17)

где 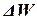- вектор изменения весов, Х(μ) – μ -тый вектор входного сигнала.

Если обозначить 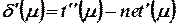, то правило обучения можно переписать в виде

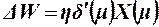(18)

6.2.2. Однослойная ИНС. Обучение искусственной нейронной сети

Распространим правило обучения персептрона на однослойную ИНС с прямыми связями и функцией Хевисайда в качестве функции преобразова-ния. Использование такой сети целесообразно для решения задачи распозна-вания n различных входных векторов. Пусть входной вектор сигнала имеет размерность m, а размерность выходного вектора при данной постановке задачи соответствует числу распознаваемых сигналов – n (рис. 6).

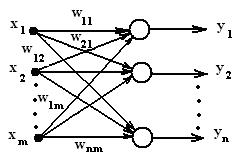
Рис. 6

При этом каждый i-тый нейрон сети соответствует модели, представ-ленной на рис.1.

Так как на вход нейронной сети может поступать любой из распозна-ваемых векторных сигналов, а также и сигналы, не подлежащие распознава-нию, то для любого нейрона необходимо обеспечить такой выбор вектора весов, при котором бы на его выходе появлялся единичный сигнал при появ-лении на его входе сигнала, на который он настроен (“полезный” для данного нейрона сигнал), и нулевой сигнал при появлении на его входе сигнала не соответствующего сигналу настройки (“мешающий” для данного нейрона сигнал). Это приводит к тому, что желаемые реакции каждого из нейронов сети должны быть разными в зависимости от входного сигнала.

В связи с этим задача обучения однослойной сети заключается в поиске таких векторов весов W_i= (w_i1,w_i2,...,w_im) и порогового значения θ_i, при ко-торых будет обеспечиваться совпадение желаемой 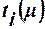и действительной реакции персептрона 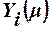на соответствующий входной вектор 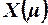,то есть при наличии на входе сети сигнала, для которого реакция i-того нейро-на должна быть единичной, необходимо выполнение условия

t´_{iжел пол} (μ) =net_{iжел пол}(μ) 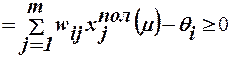, (19)

в противном случае

t´_{iжел меш} (μ) =net_{iжел меш}(μ) 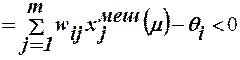, (20)

или по аналогии с предыдущим в первом случае должно выполняться соотношение

t´´_{iжел пол} (μ) =net´_{iжел пол}(μ) 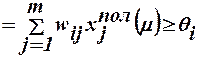, (21)

а во втором -

t´´_{iжел меш} (μ) =net´_{iжел меш}(μ) 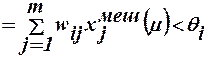, (22)

С учетом этого и выражения (17) пошаговая адаптация весов каждого нейрона выполняется с помощью правила

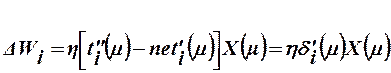(23)

где 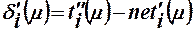- ошибка обучения i-того нейрона, (24)

t´´_i (μ)= t´´_{iжел пол} (μ) при наличии на входе i-того нейрона полез-ного сигнала и

t´´_i (μ)= t´´_{iжел меш} (μ) при поступлении на вход i-того нейрона ме-шающего сигнала,

net´_i(μ)= 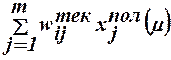при наличии на входе i-того нейрона полезного сигнала и

net´_i(μ)= 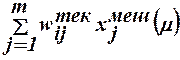при поступлении на вход i-того ней-рона мешающего сигнала,

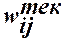- текущие значения компонентов i-того весового вектора, по-лученные на предыдущем шаге

6.2.3. Проектирование однослойной искусственной нейронной сети

Ход проектирования однослойной искусственной нейронной сети про-изводится в соответствии со следующими этапами:

1. Проводится анализ задания на проектирование. Выполняется коди-рование (при необходимости) входной информации. Определяется размер-ность входного вектора и необходимое для решения задачи распознавания число нейронов.

2. Разрабатывается структурная схема нейронной сети. Осуществляется закрепление каждого из нейронов за распознаваемым образом.

3. Выбирается правило расчета весовых коэффициентов.

4. Выбирается некоторый i-тый нейрон и образ (сигнал), для распозна-вания которого предназначается этот нейронный элемент. Определяются па-раметры, необходимые для расчета вектора весовых коэффициентов:

- коэффициент обучения выбранного нейрона. При этом необходи-мо учитывать, что большое значение коэффициента обучения может привес-ти к постоянной неустойчивости процесса обучения, а малые значения при-водят к медленной сходимости решения. Поэтому в качестве h обычно вы-бирается число меньше 1, но не очень маленькое, например, 0,6, и оно может постепенно уменьшаться в процессе обучения.

- пороговое значение θ_i. Для определенности рекомендуется выби-рать значение, равное числу единиц в сигнале, распознаваемом этим нейро-ном.

- величины t´´_{iжел пол} (μ) и t´´_{iжел меш} (μ) как θ_i + ∆ в первом случае и θ_i -∆ во втором случае. Величину ∆ рекомендуется выбирать мень-ше величины θ_i, равной, например, 1.

- так как процедура является итерационной и обеспечивает посте-пенное пошаговое приближение к желаемому результату (определению век-тора весовых коэффициентов) для сокращения времени обучения задаются максимально допустимые значения ошибок обучения δ_{max пол} и δ_{max меш}, которые должны быть значительно меньше величины ∆.

5. Осуществляют расчет вектора весовых коэффициентов выбранного нейронного элемента.

5.1. Задают начальное значение вектора весовых коэффициентов (ком-понент вектора) выбранного нейрона. Как правило на первом шаге значени-ям компонент весового вектора присваивают небольшие случайные значения в пределах от 0 до 1. (Так как в процессе обучения начальные значения кор-ректируются, то эти начальные значения могут быть выбраны одинаковыми для всех нейронов.)

5.2. На вход сети подается сигнал, характеризующий образ, для распоз-навания которого служит выбранный нейронный элемент.

5.3. С учетом заданного начального значения весового вектора для этого сигнала определяется сетевая функция

net´_i(μ)= ,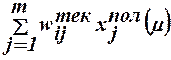

где в качестве текущих значений составляющих весового вектора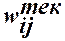

выбираются их начальные значения.

5.4. Определяется ошибка обучения в соответствии с (24).

5.5. Полученное значение ошибки обучения сравнивается с максималь-но допустимой ошибкой δ_{max пол}. Если 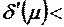δ_{max пол}, то коррекция начальных значений составляющих вектора весовых коэффициентов не про-изводится и текущему значению вектора весовых коэффициентов присваи-вается начальное значение, то есть 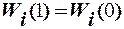. Если 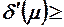δ_{max пол}, то производится первая коррекция весового вектора в соответствии с выра-жением

,

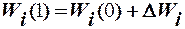где 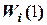- значение вектора весовых коэффициентов после первой коррек-ции,

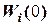- начальное значение вектора весовых коэффициентов,
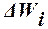определяется в соответствиис выражением(23).

5.6. На вход сети подается сигнал, характеризующий второй (меша-ющий) образ, на который реакция данного нейрона должна быть нулевой.

5.7. С учетом скорректированного значения весового вектора для этого сигнала определяется сетевая функция

net´_i(μ)= ,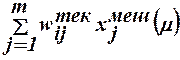

где в качестве текущих значений составляющих весового вектора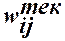

выбираются их скорректированные значения.

5.8. Определяется ошибка обучения в соответствии с (24).

5.9. Полученное значение ошибки обучения сравнивается с макси-мально допустимой ошибкой δ_{max меш}. Если 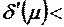δ_{max меш}, то кор-рекция значений составляющих вектора весовых коэффициентов 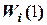не производится и текущему значению вектора весовых коэффициентов при-сваивается значение, полученное на предыдущем шаге, то есть 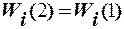. Если 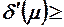δ_{max меш}, то производится вторая коррекция коррекция весового вектора в соответствии с выражением

,

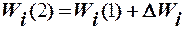где 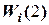- значение вектора весовых коэффициентов после второй коррек-ции,

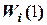- значение вектора весовых коэффициентов после первой коррек-ции.
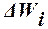определяется в соответствиис выражением(23).

5.10. Процедуры 5.6 – 5.9 повторяются для всех мешающих для дан-ного нейрона сигналов.

5.11. Если для всех шагов (как при входном полезном сигнале, так и при входных мешающих сигналах) величина ошибок меньше предельно допус-тимых (то есть конечное значение весового вектора соответствует начально-му значению), то процесс обучения нейрона заканчивается. Если хотя бы на одном шаге производилась коррекция вектора весовых коэффициентов, то осуществляется переход ко второй итерации.

Дата добавления: 2015-06-27