Методика выполнения в Microsoft Excel. Формальная математическая постановки задачи

Ограничения

Формальная математическая постановки задачи

Константы

1. Пусть m_ij – расход сырья i для изделия j, где i=1,2,3; j=1,2,3.

18 15 12

m_ij = 6 4 8

5 3 3

2. Пусть Z_i – общее количество i на складе, где i = 1,2,3.

Z₁=1000; Z₂=750; Z₃=800.

3. Пусть Р_i – цена изделия j, то есть

P_А=120; Р_В=110; Р_С=160

Переменные

1. Обозначим через x_j количество изделий j, j=1,2,3, то есть

x₁ - количество изделий А;

x₂ - количество изделий В;

x₃ - количество изделий С.

2. Обозначим через Ri расход микросхем i, где i=1,2,3, то есть

R₁ - расход сырья I;

R₂ – расход сырья II;

R₃ – расход сырья III.

3. Обозначим через N общее количество изделий А,В и С.

Решение

1.Зададим математическую модель расхода сырья

R_i = _j=1³∑ x_im_ij, где i=1,2,3.

Или

R₁=x₁m₁₁+x₂m₁₂+x₃m₁₃ R₁=18x₁+15x₂+12x₃

R₂=x₁m₂₁+x₂m₂₂+x₃m₂₃ R₂=6x₁+4x₂+8x₃

R₃=x₁m₃₁+x₂m₃₂+x₃m₃₃ R₃=5x₁+3x₂+3x₃

2. Зададим математическую модель нахождения общего цены всех

изделий N = _j=1³∑ x_jP_j. Его максимизация является целью решения за-

дачи. Следовательно, целевая функция будет иметь вид:

N = _j=1³∑ x_jP_j →max

N=120x₁+110x₂+160x₃→max

1. Расход ткани не должен превышать ее общее количество

R₁ ≤ Z₁ R₁=18x₁+15x₂+12x₃≤1000 (для сырья I)

R₂ ≤ Z₂ или R₂=6x₁+4x₂+8x₃≤750 (для сырья II)

R₃ ≤ Z₂ R₃=5x₁+3x₂+3x₃≤800 (для сырья III)

2. Количество выпускаемых изделий должно быть целым числом.

3. Поскольку x1, x2, x3 выражают объем выпускаемых изделий, то

они не могут быть отрицательны, то есть

x1≥0; x2≥0; x3≥0.

1.

Вид сырья	Норма расхода (м) на одно изделие вида	Общее количество ткани (м)	Расход
A	B	C
I					=СУММПРОИЗВ(B3:D3;$B$7:$D$7)
II					=СУММПРОИЗВ(B4:D4;$B$7:$D$7)
III					=СУММПРОИЗВ(B5:D5;$B$7:$D$7)
Цена одного изделия, руб.
План				=СУММПРОИЗВ(B7:D7;B6:D6)
целевое значение
ограничение ресурсов
расход
изменяемые значения

2.

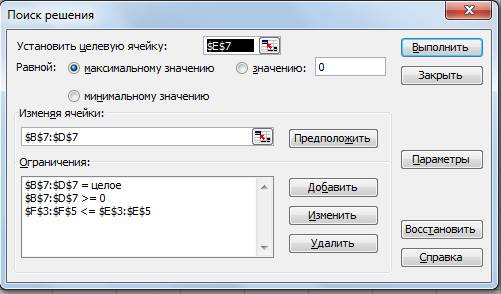
3.

Вид сырья	Норма расхода (м) на одно изделие вида	Общее количество ткани (м)	Расход
A	B	C
I
II
III
Цена одного изделия, руб.
План
целевое значение
ограничение ресурсов
расход
изменяемые значения

Дата добавления: 2015-06-27