BF (Best Fit - наилучший остаток) алгоритм

FFD алгоритм.

FF алгоритм.

Один из подходов к получению приближенного решения задачи о раскладке по ящикам предлагает упаковывать первый подходящий предмет.

Стратегия состоит в том, что ящики просматриваются поочередно, пока не найдется ящик, в котором достаточно свободного места для упаковки очередного предмета.

FirstFit (Size, N, Bin)

// Size – список размеров предметов

// N – число предметов; Bin(N) – размещение различных предметов

// Used – занятый объем ящика

for i=1 to N do

Bin[i]0

endfor

For item=1 to N do

BinLoc1

while (used(BinLoc)+Size(item))>1 do

// ищем подходящий ящик

BinLocBinLoc+1

endwhile

Bin(item)BinLoc

// занимаем найденный ящик

Used[BinLoc]Used[BinLoc]+Size[item]

endfor

Пример 1. Например, так будет происходить упаковка предметов размером (0.5, 0.7, 0.3, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.5) в ящики единичного объема.

В 1-ый ящик попадут (0.5, 0.3, 0.1), во второй – (0.7, 0.2), в третий (0.9), четвертый (0.6, 0.4), в пятый (0.8), и в шестой (0.5), то есть всего понадобится 6 ящиков.

Для этого алгоритма m_min ≥ [SS_i ]+1, где [SS_i ] – целая часть суммы объемов предметов.

В другом варианте этого алгоритма список предметов сначала сортируется по убыванию размера (в неубывающем порядке), а затем они раскладываются поочередно в первый подходящий ящик.

Для вышеприведенного примера этот алгоритм дает оптимальное решение.

Пример 2. Отсортированный по неубыванию список предметов (0.9, 0.8, 0.7, 0.6, 0.5, 0.5, 0.4, 0.3, 0.2, 0.1). Раскладка происходит в 5 ящиков:

1 – (0.9, 0.1) 2 – (0.8, 0.2) 3 – (0.7, 0.3)

4 – (0.6, 0.4) 5 – (0.5, 0.5)

Однако модифицированный алгоритм не всегда приводит к лучшим результатам, чем обычный.

Пример 3. Набор предметов (0.2, 0.6, 0.5, 0.2, 0.8, 0.3, 0.2, 0.2).

По первому способу упаковка произойдет в 3 ящика:

(0.2, 0.6, 0.2), (0.5, 0.3, 0.2) и (0.8, 0.2)

По второму способу для отсортированного списка (0.8, 0.6, 0.5, 0.3, 0.2, 0.2, 0.2, 0.2) получаем 4 ящика:

(0.8, 0.2), (0.6, 0.3), (0.5, 0.2, 0.2) и (0.2).

Анализ показывает, что в среднем стратегия укладки в первый подходящий ящик по отсортированному списку приводит к числу ящиков, превышающему оптимальное, в среднем на 50% (т.е. если для оптимальной укладки достаточно 10 ящиков, то результат алгоритма будет около 15). Если список предварительно не сортировать, то дополнительные расходы составят в среднем 70%, то есть при оптимальном числе ящиков 10, алгоритм сгенерирует укладку в 17 ящиков.

Данный алгоритм помещает всякий предмет таким образом, чтобы после его укладки в ящике оставалось как можно меньше места. Укладка в новый ящик происходит только в том случае, если очередной объект не помещается ни в какой из имеющихся ящиков.

Для вышеприведенного набора предметов (0.5, 0.7, 0.3, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.5) упаковка данным способом приведет к минимальному числу ящиков. В первый ящик попадает предмет объемом 0.5, второй предмет (объем 0.7) в этот ящик не помещается и занимает второй ящик. Предмет объемом 0.3 может быть размещен и в первом, и во втором ящике. Свободное место, остающееся при этом в первом ящике – 0.2, а во втором – 0. Поэтому этот предмет будет размещен в ящике 2. Далее, следуя вышеприведенному алгоритму, мы получаем оптимальную упаковку, такую же, как и в примере 2 для этого набора.

8.2.4. Приближения в задаче об упаковке рюкзака

Приближенный алгоритм упаковки рюкзака представляет собой простой жадный алгоритм, выбирающий наилучшее соотношение стоимости к размеру.

На первом этапе список объектов должен быть отсортирован по удельной стоимости (отношение стоимости к объему).

В таблице 8.2 приведен пример списка объектов, каждый из которых задан парой (вес, стоимость), и соответствующий отсортированный список.

Табл. 8.2 Пример списка объектов

Исходный список	(25,50)	(20,80)	(20,50)	(15,45)	(30/105)	(35,35)	(20,10)	(10,45)
Удельная стоимость			2.5		3.5		0.5	4.5
Отсортированный список	(10,45)	(20,80)	(30/105)	(15,45)	(20,50)	(25,50)	(35,35)	(20,10)

На втором этапе начинается заполнение рюкзака последовательно идущими элементами отсортированного списка объектов. Если очередной объект не входит, то он отбрасывается, и происходит переход к следующему объекту. Эти действия повторяются до тех пор, пока рюкзак не будет заполнен или будет исчерпан список объектов.

Так, для списка, приведенного в таблице 8.2, при заданной емкости 80, в рюкзак будут помещены объекты (10,45), (20,80), (30,105), (15,45). Стоимость упаковки при этом – 275, заполненный объем – 75.

Это не оптимальное решение. Так, первые 3 элемента с добавкой пятого дадут объем 80 и стоимость – 280.

Алгоритмы точного решения данной задачи будут приведены в следующей главе.

8.3. Вопросы для самопроверки

Определение классов Р, NP, NP–полных классов задач.

Примеры NP–полных задач.

Решить приближенно задачу коммивояжера для графа:

Из\До

Эвристические алгоритмы раскладки по ящикам.

Приближения в задаче об упаковке рюкзака.

9. Динамическое программирование

Ричард Беллман ввел понятие динамического программирования для характеристики алгоритмов, действующих в зависимости от меняющейся ситуации [6]. Ряд иллюстративных примеров в классической книге Р. Беллмана и Р.Дрейфуса "Прикладные задачи динамического программирования" открывает задача оптимальной по стоимости одномерной упаковки рюкзака. Повышенный интерес к этой задаче, равно как и к ее многочисленным модификациям, связан как с разнообразными практическими областями применения, так и с отсутствием "быстрых" алгоритмов решения. Метод динамического программирования, хотя и позволил существенно сократить полный перебор вариантов, но реализующие этот метод алгоритмы не являются полиномиальными относительно длины входа.

Реализация метода динамического программирования, обеспечивающего точное решение задачи одномерной упаковки, может быть осуществлена следующими двумя принципиально разными алгоритмами:

– табличным алгоритмом, опирающимся на вычисление и хранение векторов оптимальной упаковки для всех последовательных целочисленных значений объема;

– рекурсивным алгоритмом, непосредственно реализующим основное функциональное уравнение Беллмана для задачи одномерной оптимальной упаковки.

Напомним общую постановку задачи одномерной оптимальной по стоимости упаковки.

Пусть задано множество типов грузов:

Y = { y_i }, 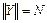, y_i ={ v_i, c_i }, i Î {1,2 ,…,N },

где каждый элемент y_i обладает целочисленным линейным размером – v_i, или "объемом" в общепринятых терминах задач упаковки, и ценовой характеристикой – c_i, которая содержательно отражает практически значимые предпочтения для загрузки объектов данного типа.

Так же целочисленным значением задан основной объем упаковки V. В классической постановке элементы y_i называются типами грузов [6]. Для описания количества загружаемых в объем V элементов y_i вводится в рассмотрение следующий характеристический вектор:

X = { x_i }, x_i – неотрицательное целое, i Î { 1,2,…,N } (9.1)

Значение компонента вектора x_i = k соответствует загрузке k элементов типа y_i в объем V.

Среди всех возможных упаковок объема V грузами из Y должна существовать, по крайней мере, одна упаковка, максимизирующая суммарную стоимость в объеме V, что приводит к следующей постановке задачи:

Максимизировать линейную форму:

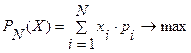, (9.2)

при выполнении следующего условия:

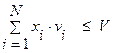(9.3)

Содержательно условие (9.3) означает, что суммарный объем, занимаемый грузами всех типов в количествах, указанных характеристическим вектором X, не должен превышать общего объема упаковки.

Один из вариантов точного решения задачи методом динамического программирования – это табличный алгоритм [6], позволяющий получить набор оптимальных решений не только для заданного объема V, но и для всех промежуточных дискретных значений этого объема.

Обозначим вектор оптимальной упаковки для объема v элементами y_j,
y_i Î {1, 2 ,…,k }, через 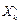, а через f_k (v) – стоимость оптимальной упаковки в этом объеме. В силу принципа оптимальности 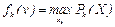, а порядок предъявления элементов y_j не является существенным.

Решение табличным алгоритмом осуществляется на основе функционального уравнения метода динамического программирования:

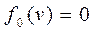
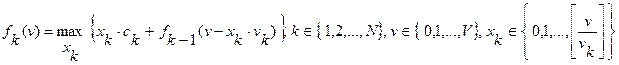
Результатом решения задачи является набор оптимальных значений целевой функции f_N (v) и соответствующих векторов оптимальной упаковки 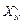для всех объемов v от 0до V исходными элементами (типами грузов) из Y. Табличный способ позволяет получить оптимальные решения для всех промежуточных объемов упаковки.

Пример формирования таблицы оптимальной упаковки для исходных данных оптимального дохода в табл. 9.1, представлен в табл. 9.2.

Табл. 9.1. Таблица исходных данных.

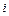
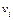
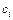
Табл. 9.2. Таблица оптимального дохода.

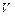
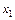
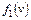
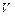
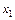
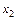
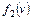
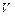
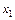
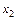
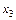
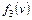
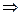
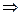
Ниже представлена реализация данного алгоритма:

инициализация начальных условий

часть1 --------------------

цикл от i = 1 до V // формирование таблицы оптимального дохода для
грузов типа 1

x[1, i] = i/boxV[1]

x1[1, i] = x[1, i]

f[i] = x[1, i]*boxC[1]

цикл от i = 2 до N // цикл по количеству типов грузов

Vi=boxV[i]

Ci=boxC[i]

цикл от j = 1 до V // цикл по объему упаковки

maxKol = 0; maxC = f[j]

если Vi <= j то

z = j/Vi // максимальное количество 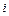-го типа
груза в объеме j

часть2 ---------------------

цикл от l = 1 до z // цикл нахождения максимальной стоимости

если (maxC < (Ci*l+f[j-l*Vi])) то

maxC = Ci*l+f[j-l*Vi]

maxKol= l

часть3 ---------------------

цикл от l=1 до i-1

x[l, j] = x1[l, j-maxKol*Vi]

x[I, j]=maxKol

часть4 ---------------------

цикл от l=1 до i

цикл от j=1 до V

x1[l, j]=x[l, j]

цикл от l=1 до V // цикл подсчета общей стоимости

sum = 0

часть5 ---------------------

цикл от j=1 до j<=i

sum = sum + x[j][l]*boxC[j]

f[l]=sum

В данном алгоритме части 1, 3, 4, 5 зависят только от , 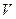и их трудоемкость может быть подсчитана заранее , , ,

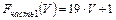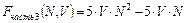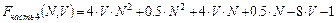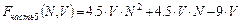
Трудоемкость части2 данного алгоритма в равна среднем 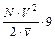элементарных операций.

Учитывая циклы по количеству типов грузов, по объему упаковки и цикла подсчета общей стоимости получаем среднее количество элементарных операций для данного алгоритма:

.

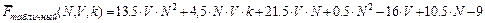10. Метод ветвей и границ

Алгоритм ветвей и границ хорошо работает в задаче коммивоя­жера, рассмотренной в разделе 8.1.1. В данном разделе изложение будет вестись на примере задачи коммивояжера.

Метод, известный как метод ветвей и границ, исследует древовидную модель простран­ства решений. Примен и м для широкого круга дискретных комбина­торных задач. Алгоритмы ветвей и границ ориентированы в большей степени на оптимизацию. Например, в решаемой задаче определена числовая функция стоимости для каждой из вершин, появляющихся в дереве поиска. Цель — найти конфигурацию, на которой функция стоимости достигает максимального или минималь­ного значения.

Напомним, что задача заключается в нахождении в торговом участке коммивояжера тура из N городов с наименьшей стоимостью. Каждый город входит в тур только один раз. В терминах графов в графе городов надо найти покрывающий цикл наименьшей стоимости. Имеется матрица С, каждый элемент которой c _ij равен стоимости (обычно в единицах времени, денег или расстояния) прямого проезда из города i в город j. Задача называется симметричной, если c _ij = c _ji для всех i и j, т. е. если стоимость проезда между каждыми двумя городами не зависит от направления. Предположим, что сii=∞ для всех i.

Алгоритмы ветвей и границ для задачи коммивояжера могут быть сформулированы разными способами. Авторы излагаемого алгорит­ма - Литл, Мерти, Суини и Карел. Это своего рода классика [1].

Во-первых, рассмотрим ветвление. На рис. 10.1, а показана мат­рица стоимостей для асимметричной (несимметричной) задачи комми­вояжера с пятью городами, представленной на рис.10.1, 6. Обратите внимание на то, что используется ориентированный граф, чтобы ука­зать стоимости, так как стоимость проезда из города i прямо в город j не обязательно такая же, как стоимость проезда из города j в город i. Корень поискового дерева будет соответствовать множеству «всех возможных туров», т. е. эта вершина представляет множество всех 4! возможных туров в данной задаче с пятью городами. В общем случае для любой асимметричной задачи с N городами корень будет представлять полное множество R всех (N —1 )! возможных туров. Ветви, выходящие из корня, определяются выбором одного ребра, скажем (t,j). Наша цель состоит в том, чтобы разделить множество всех туров на два множества: одно, которое, весьма вероятно, содер­жит оптимальный тур, и другое, которое, вероят но, не содержит. Для этого выбираем ребро (i, j); оно, как мы надеемся, входит в оп­тимальный тур, и разделяем R на два множества { i, j } и { i, j }. В мно­жество {i, j) входят туры из R, содержащие ребро (i, j), а в { i, j } — не содержащие (i,j).

	∞
		∞
			∞
				∞
					∞

а)

б)

Рис. 10.1.Задачакоммивояжера:
(а) матрица стоимостей; (б) граф из пяти городов.

Предположим, в данном примере производится ветвление на ребре (i, j)=(3,5), имеющем наименьшую стоимость во всей матрице. Корень и первый уровень дерева пространства решений будут тогда такими,как показано на рис.10.2. Заметим, что каждый тур из R содержится только в одном множестве уровня 1. Если бы мы как-то могли сделать вывод, что множество {3,5} не содержит оптимального тура, то нам нужно было бы исследовать только множество {3, 5}.

Затем разделяем множество {3, 5} таким же образом, как и множе­ство R. Следующее по дешевизне ребро в матрице – это ребро (2, 1) со стоимостью c₂₁=5. Поэтому можно разделить множество {3, 5} на туры, включающие ребро (2, 1), и туры, не включающие этого ребра; это показано на уровне 2 на рис.10.2. Путьот корня к любой вершине дерева выделяет определенные ребра, которые должны или не должны быть включены в множество, представленное вершиной дерева. Например, левая вершина уровня 2 на рис.10.2 представляет множе­ство всех туров, содержащих ребро (3, 5) и не содержащих ребра (2, 1). Вообще, если X – вершина дерева, а
(i, j) – ребро ветвления, то обозначим вершины, непосредственно следующие за X, через Y и ` Y. Множество Y обозначает подмножество туров из X с ребром (i,j), а множество ` Y – подмножество X без (i, j).

Проведенное обсуждение дает некоторое пред­ставление о том, что подразумевается под ветвлением. Перед тем как приступить к полному описанию алгоритма для задачи коммивояжера, поясним, что подразумевается под вычислением границ.

С каждой вершиной дерева мы связываем нижнюю границу стои­мости любого тура из множества, представленного вершиной. Вычис­ление этих нижних границ — основной фактор, дающий экономию усилий в любом алгоритме типа ветвей и границ. Поэтому особое внимание следует уделить получению как можно более точных границ. Причина этого следующая. Предположим, что мы построили конкрет­ный полный тур со стоимостью т. Если нижняя граница, связанная с множеством туров, представленных вершиной v_k, равна М≥т, то до конца процесса поиска оптимального тура не нужно рассматривать вершину v_k и все следующие за ней (почему?).

Основной шаг при вычислении нижних границ известен как при­ведение. Оно основано на следующих двух соображениях:

1. В терминах матрицы стоимостей С каждый полный тур содержит только один элемент (ребро и соответствующую стоимость) из каждого столбца и каждой строки. Заметим, что обратное утверждение не всегда верно. Множество, содержащее один и только один элемент из каждой строки и из каждого столбца С, не обязательно представляет тур. Например, в задаче, изображенной на рис.10.4 множество {(1,5), (5,1), (2,3), (3,4), (4,2)} удовлетворяет этому условию, но не образует тура.

2. Если вычесть константу h из каждого элемента какой-то строки или столбца матрицы стоимостей С, то стоимость любого тура при новой матрице С ’ровно на h меньше стоимости того же тура при матрице С. Поскольку любой тур должен содержать ребро из данной строки или данного столбца, стоимость всех туров уменьшается на h. Это вычитание и называется приведением строки (или столбца).

Пусть t — оптимальный тур при матрице стоимостей С. Тогда стоимостью тура t будет

Если С ’получается из С приведением строки (или столбца), то t дол­жен оставаться оптимальным туром; при С’ и

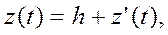
где z ' (t) — стоимость тура t при С’.

Под приведением всей матрицы стоимостей С понимается следую­щее. Последовательно проходим строки С и вычитаем значение наи­меньшего элемента h_i каждой строки из каждого элемента этой строки. Потом то же самое делаем для каждого столбца. Если для некоторого столбца или строки h_i= 0, то рассматриваемый столбец или строка уже приведены, и тогда переходим к следующему столбцу или строке.

Полученную в результате матрицу стоимостей назовем приведенной из С. На рис.10.3 показано приведение матрицы стоимостей, изобра­женной на рис.10.1, а. Значения h_i даны в конце каждой строки и столбца (строки и столбцы последовательно пронумерованы).

	∞					h 1=25
		∞				h 2=5
			∞			h 3=1
				∞		h 4=6
					∞	h 5=7
	h 6=0	h 7=0	h 8=0	h 9=3	h 10=0

h = 25+5+1+6+7+3 = 47

Рис.10.3 Приведение матрицы стоимостей, показанной на рис. 10.1, а.

Общее приведение составляет h =47 единиц. Следовательно, ниж­няя граница стоимости любого тура из R также равна 47, т. е.

z (t) =h+z’ (t) ≥h= 47

так как z '(t)≥0 для любого тура t при приведенной матрице С ’. Эта граница указана около корня дерева на рис.10.2.

По определению ребро (3, 5) содержится в каждом туре множе­ства
{3, 5}. Этот факт препятствует выбору ребра (5, 3), так как ребра (3, 5) и (5, 3) образуют цикл, а это не допускается ни для какого тура.

Ребро (5, 3) исключаем из рассмотрения, положив с₅₃ = ∞. Строку 3 и столбец 5 также можно исключить из дальнейшего рассмотрения по отношению к множеству {3, 5}, потому что уже есть ребро из 3 в 5. Часть приведенной матрицы стоимостей, показанной на рис.10.3, которая будет хоть сколько-нибудь полезна для дальнейшего поиска на множестве туров {3, 5}, показана на рис.10.4, а. Она может быть приведена к матрице стоимостей, показанной на рис.10.4, б с h = 15. Теперь нижняя граница для любого тура из множества
{3, 5} равна 47+15=62; она указана около вершины {3, 5} на рис.10.2.

	∞
		∞
				∞
			∞

	∞
		∞
				∞
			∞

Дата добавления: 2015-06-27