Краткая теория

Работа 5. Второй закон Ньютона

Н.В. Чербунина, А.Г. Рипп

Цель работы

Целью работы является экспериментальная проверка второго закона Ньютона с помощью машины Атвуда.

1.

Рис. 1.1. Машина Атвуда

Груз 2

Блок

Груз 1

Перегрузок

Подставка

Стойка с линейкой

m ₀

m ₀

Машина Атвуда

Устройство машины Атвуда показано на рисунке 1.1. На вертикальной стойке закреплён в подшипнике блок, так что он может вращаться вокруг своей оси. На блок повешена нить, к концам которой прикреплены два одинаковых груза (груз 1 и груз 2). На один из грузов можно положить дополнительный груз (перегрузок), масса которого m значительно меньше массы m ₀ каждого из грузов. На стойке закреплена линейка, позволяющая измерять координаты грузов и пройденный ими путь.

Без перегрузка система уравновешена. Это значит, что если не толкать грузы или блок, то все части машины Атвуда будут неподвижны. Перегрузок нарушает равновесие, в результате чего грузы начинают двигаться (один – вверх, другой – вниз), а блок начинает вращаться. Характер движения грузов и блока можно выяснить, используя законы динамики. Главный из них – второй закон Ньютона. Он состоит в том, что силы, действующие на материальный объект, влияют на скорость его движения 𝑣, изменяя её. При этом быстрота изменения скорости, то есть ускорение 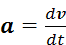, зависит от внешних сил следующим образом:

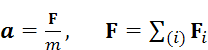, (2.1)

где F _i – внешние силы, действующие на объект, m – масса объекта. Сумму внешних сил F называют равнодействующей силой.

Есть ещё одна формулировка второго закона Ньютона:

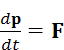, (2.2)

где p – импульс объекта. В релятивистской механике, то есть при скоростях объекта, сравнимых со скоростью света, правильной является только вторая формулировка, то есть формула (2.2). В нерелятивистской (классической) механике обе формулировки считаются эквивалентными, иначе говоря, вытекающими друг из друга. При этом в большинстве случаев используется первая формулировка, то есть (2.1). Грузы в машине Атвуда двигаются со скоростями, на много порядков меньшими, чем скорость света, поэтому для них применима классическая механика.

Рассмотрим, что даёт применение второго закона Ньютона к отдельным элементам машины Атвуда. Этих элементов три: груз 1, груз 2 с перегрузком и блок.

Рис. 2.1. Силы и ускорения

m ₀

m ₀

G₁

T₁

T'₁

G₂

T'₂

T₂

R

a ₁

a ₂

X

Груз 1. На него действуют две противоположно направленные силы: сила натяжения нити T ₁ и сила тяжести G ₁ = m ₀ g. – см. рисунок 2.1. В результате груз движется вверх с ускорением a ₁. Запишем второй закон Ньютона.

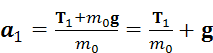. (2.3)

Перейдём от векторов к числам, для чего запишем уравнение (2.3) в проекциях на вертикальную ось OX.

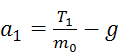. (2.4)

Груз 2. На него тоже действуют две противоположно направленные силы: сила натяжения нити T ₂ и сила тяжести
G ₂ = (m ₀ + m) g. В результате груз движется вниз с ускорением a ₂. Запишем для этого груза второй закон Ньютона.

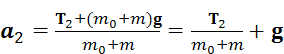. (2.5)

В проекциях на OX уравнение (2.5) имеет вид:

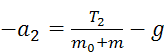. (2.6)

Блок. На него действуют три вертикально направленные силы: силы натяжения нитей T '₁ и T '₂ и сила реакции опоры R, действующая со стороны подшипника. Блок никуда не движется, его движение – вращательное. Поэтому, во-первых, скорость и ускорение его центра масс равны нулю, так что применение к блоку второго закона Ньютона приводит к выводу, что сумма сил (T '₁ + T '₂ + R) равна нулю, так что сила реакции компенсирует силы натяжения. Во-вторых, блок вращается с угловым ускорением e, найти которое можно, применив основной закон динамики вращательного движения. Изучение этого закона не входит в задачи данной лабораторной работы, поэтому отметим без доказательства, что применение основного закона динамики вращательного движения к лёгкому блоку, масса которого значительно меньше массы грузов, приводит к выводу:

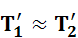. (2.7)

С другой стороны, каждая нить тянет оба своих конца с одной и той же силой, так что

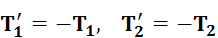. (2.8)

Из (2.7) и (2.8) следует, что

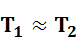. (2.9)

Учтём ещё, что грузы двигаются хотя и в разные стороны, но с одной и той же скоростью 𝑣 и, значит, с одним и тем же ускорением a, так что

s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>=a</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 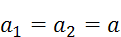. (2.10)

В результате уравнения (2.4) и (2.6) можно записать в виде следующей системы:

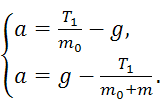(2.11)

В этой системе уравнений две неизвестные: ускорение грузов a и сила натяжения T ₁. Решая систему, получим:

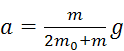. (2.12)

Так как масса перегрузка m на порядок меньше массы каждого из грузов, то в знаменателе формулы (2.12) можно отбросить малое слагаемое m, и тогда получится следующий результат.

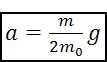. (2.13)

Согласно этой формуле, ускорение движения грузов a прямо пропорционально массе перегрузка m и обратно пропорционально массе грузов 2 m ₀. Этот факт можно проверить экспериментально. В данной лабораторной работе предлагается исследовать зависимость ускорения движения грузов a от массы перегрузка m. Если экспериментальная зависимость a (m) окажется действительно прямо пропорциональной, то это будет косвенным подтверждением второго закона Ньютона, так как вывод формулы (2.13) основан именно на втором законе Ньютона. Критерием того, что a прямо пропорционально m, является график зависимости a (m): прямая линия, проходящая через начало координат. Таким образом, надо провести серию измерений ускорения грузов при разных значениях m, а затем построить график экспериментальной зависимости a (m). Если на этом графике экспериментальные точки выстроятся вдоль прямой линии, проходящей через начало координат, то это и будет подтверждением формулы (2.11). Заметьте: утверждение, что экспериментальные точки лежат на прямой линии, надо понимать не буквально. Считается, что экспериментальные точки лежат на прямой линии, если на графике можно провести прямую линию, которая пересечёт планки погрешностей всех этих точек.

Теперь надо выбрать способ измерения массы перегрузка m и ускорения грузов a.

Перегрузок состоит из одного или нескольких элементарных грузов. Масса каждого элементарного груза уже измерена и написана на нём.

Для измерения ускорения можно воспользоваться уравнением кинематики равноускоренного движения материальной точки:

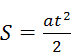, (2.14)

где S – путь, пройденный за время t точкой, которая движется равноускоренно с ускорением a. Если измерять время падения t груза 2 с заданной высоты h на лабораторный стол, то S = h и тогда из (2.14) следует:

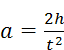. (2.15)

Эта формула и определяет способ косвенного измерения ускорения грузов a.

Если опыты будут успешными и в итоге удастся провести по экспериментальным точкам[1] прямую линию, то можно будет получить дополнительную информацию: измерить массу груза m ₀. Для этого достаточно взять на прямой любую точку – не экспериментальную, а любую точку, принадлежащую проведённой экспериментальной прямой, измерить её координаты (m; a) и затем, использовав формулу (2.13), определить значение m ₀. Масса груза указана на нём: 100 г. Поэтому измерение массы груза и сравнение результата с числом 100 г является дополнительным способом экспериментальной проверки теоретической формулы (2.13).

Дата добавления: 2015-06-28