Лабораторная работа №6. Доверительные области и доверительные интервалы

Доверительной областью называется область, внутри которой случайная величина находится с вероятностью не менее заданной, а доверительным интервалом – границы этой области.

Задача 1. Произведено 20 опытов над величиной Х. Результаты приведены в таблице:

i	xi	i	xi
	10.5		10.6
	10.8		11.3
	11.2		10.5
	10.9		10.7
	10.4		10.8
	10.6		10.9
	10.9		10.8
	11.0		10.7
	10.3		10.9
	10.8		11.0

Требуется.найти оценку математического ожидания 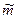и и построить для него доверительный интервал вероятности β=0.8.

1.Составляем из таблицы вектор X (на рис.1 для экономии места часть этого вектора приведена в транспонированном виде). Вычисляем с помощью встроенной функции mean среднее арифметическое – оценку математического ожидания, а с помощью встроенной функции stdev – оценку среднеквадратического отклонения..

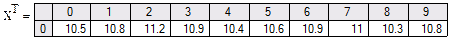
Рис.1 Ввод наблюдений и вычисление числовых характеристик.

Вычисленное значение среднего является случайной величиной (например, если увеличить число опытов, то оно изменится). И как для любой случайной величины, мы можем построить для него математическое ожидание и среднеквадратическое отклонение.

Теперь мы должны найти для него такой отрезок на оси х, внутри которого эта случайная величина находится с вероятностью 0,8.

Для решения этой задачи нужно найти такой интервал ε относительно оценки математического ожидания 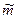, внутри которого с вероятностью 0.8 расположено истинное значение математического ожидания m:

Из курса теории вероятностей известно, что для этого необходимо вычислить обратную функцию распределения исследуемой случайной величины. Наше среднее является суммой независимых одинаково распределенных случайных величин Х_i (i=1..20) и, согласно центральной предельной теореме, при достаточно большом числе опытов ее закон распределения близок к нормальному. На практике, даже при относительно небольшом числе слагаемых (порядка 10 – 20) закон распределения суммы можно считать нормальным. Поэтому будем считать, что m – нормально распределенная случайная величина. В этом случае необходимо использовать обратную функцию Лапласа Φ^-1.

В Маткаде имеется встроенная функция qnorm(p,m,σ ), являющаяся обратной функцией нормального распределения. Здесь р – заданная вероятность, m - математическое ожидание, а σ –среднеквадратическое отклонение нормально распределенной случайной величины. Функция qnorm возвращает отрезок -∞ - х, оси абсцисс, на котором находится случайная величина х с заданной вероятностью р.

Нас интересует отрезок 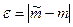, внутри которого с вероятностью 0,8 должно находиться математическое ожидание m.

Для лучшего понимания, что нам необходимо сделать, рассмотрим рис.2

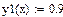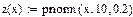
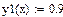
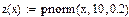
Рис.2. Доверительный интервал для нормальной функции распределения.

На этом рисунке кривая – функция распределения нормально распределенной случайной величины с математическим ожиданием m=10 и среднеквадратическим отклонением σ=0,2. Функция распределения F(x) показывает вероятность попадания случайной величины х на отрезок оси абсцисс (-∞, х). Из рисунка видно, что эта вероятность для х= m равна 0.5. Нам нужно найти такие отрезки на оси х, границы которых соответствуют вероятностям 0,5+0,4 и 0,5-0,4. Их длину мы обозначим через ε1 и ε2. Эти вероятности обозначены на рисунке пунктирными горизонтальными линиями. Нахождение отрезков и границ доверительной области в Маткаде показано на рис.3. В первой строке производится вычисление верхнего интервала и верхней границы доверительной области, во второй – нижнего интервала и нижней границы области.

Задача решена.

.

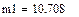
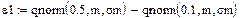
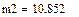
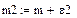
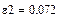
Рис.3. Вычисление отрезков ε1 и ε2 и границ доверительной области.

Дата добавления: 2015-06-27