Решение в Маткаде

Проверка статистических гипотез в пакете Маткад.

Произведено 500 наблюдений. Результаты наблюдений сведены в статистический ряд:

Интервалы Наблюдений	-4-;3	-3;-2	-2;-1	-1;0	0;1	1;2	2;3	3;4
Число наблюдений в данном интервале
Частота m/n	0.012	0.05	0.144	0.266	0.240	0.176	0.092	0.02

Задано среднее этих наблюдений m=0.2 и среднеквадратическое отклонение s=1.5.

Требуется построить гистограмму этого ряда, выбрать в качестве теоретического нормальное распределение и проверить его согласованность со статистическим распределением. В качестве параметров теоретического нормального распределения выбрать статистическое среднее и статистическое среднеквадратическое отклонение.

Гистограмма для этой задачи была построена в лабораторной работе №6 модуля 1. Поэтому здесь только приводятся ее график и векторы интервалов и частот.

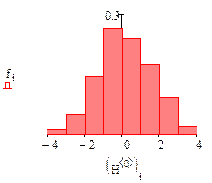
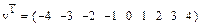
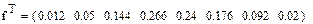
Рис.4. График гистограммы и векторы интервалов и частоты

После построения гистограммы с помощью встроенной функции dnorm(x, 0.2,1.35) строим график нормального закона распределения и вычисляем вероятности попадания случайной величины в каждый интервал. Как известно, эта вероятность равна интегралу от кривой распределения в пределах границ участка.

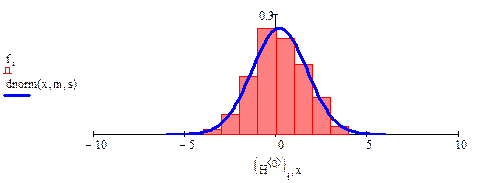
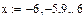
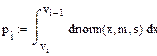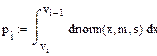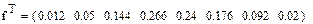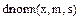
Рис.5.График гистограммы и теоретического нормального распределения

Далее (см. рис.6), вычисляем значение χ² (мы обозначили его через U), оно равно 3.899, и вызываем встроенную функцию Маткада pchisq. Если ввести в нее вычисленное значение U и число «степеней свободы», то в ответ получим вероятность противоречивости гипотезы о нормальном распределении наших наблюдений. В нашем случае число степеней свободы равно пяти, так как у нас восемь интервалов, и мы накладываем три условия:

1. сумма теоретических вероятностей равна 1,

2. задаемся математическим ожиданием теоретического распределения,

3. задаемся среднеквадратическим отклонением теоретического распределения.

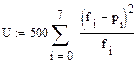Как известно, число степеней свободы равно разности числа интервалов и числа условий. В результате мы получили вероятность р=0.436. Это вероятность несоответствия наблюдений нашей гипотезе.

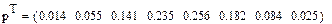
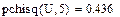
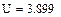
Рис.6. Вычисление вероятности несоответствия наблюдений гипотезе о нормальности

Следовательно, вероятность соответствия рсоотв. = 1- pchisq = 0.564

Это достаточно хорошая вероятность того, что наши наблюдения распределены нормально.

Дата добавления: 2015-06-27