Минимаксный принцип поиска решений

Алгоритмы поиска пути на И/ИЛИ- графах могут использовать стратегии поиска в глубину и ширину, однако, для большинства игр, дерево игры имеет большое количество позиций, что приводит к комбинаторному взрыву при реализации просмотра всех вершин дерева решений.

Основной подход к организации поиска на игровых деревьях использует оценочные функции. Оценочная функция используется для вычисления оценки текущего состояния игры.

Для выбора следующего хода используется простой алгоритм:

· найти всевозможные состояния игры, которые могут быть достигнуты за один ход;

· используя оценочную функцию, вычислить оценки состояний;

· выбрать ход, ведущий к позиции с наивысшей оценкой.

Если оценочная функция была бы совершенной, то есть ее значение отражало бы какие позиции ведут к победе, а какие – к поражению, то достаточно было бы просмотра вперед на один шаг. Обычно совершенная оценочная функция неизвестна, поэтому стратегия выбора хода на основе просмотра на один шаг вперед не дает хорошего результата, поэтому используется стратегия просмотра на несколько шагов вперед.

Станодартный метод определения оценки позиции, основанный на просмотре вперед нескольких слоев игрового дерева, назывыается минимаксным алгоритмом.

Минимаксный алгоритм предполагает, что противник из нескольких возможных ходов сделает выбор, лучший для себя, то есть худший для игрока. Поэтому целью игрока является выбор такого хода, который даст максимальную оценку позиции, возможной после лучшего хода противника, то есть минимизирующего оценку позиции противника. Отсюда название – минимаксный алгоритм. Число слоев игрового дерева, просматриваемых при поиске, зависит от доступных ресурсов. На последнем слое используется оценочная функция.

В предположении, что оценочная функция выбрана разумно, алгоритм будет давать тем лучшие результаты, чем больше слоев просматривается при поиске.

Пусть мы имеем следующее дерево игры:

a

игрок

c

t8

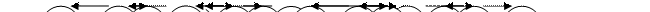
Задана некая оценочная функция j(P_k), где P_k- некоторая игровая ситуация.

Предположим, что игрок максимизирует свой выигрыш, а противник минимизирует свой проигрыш. Вариант решения, образованный минимаксной стратегией движения по дереву игры, будем называть основным вариантом решения.

Если существует оценочная функция, то можно ввести внутреннюю функцию j(P_k) такую, что:

j(p_k)=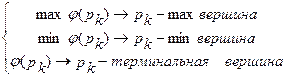

trace

domains

pozic = symbol

spoz = pozic*

database

xod (pozic, spoz)

xod_min (pozic)

xod_max (pozic)

predicates

minmax (pozic, pozic, integer)

best (spoz, pozic, integer)

oc_term(pozic, integer)

vibor(pozic, integer, pozic, integer, pozic, integer)

clauses

xod (a, [b,c]).

xod (b, [d,e]).

xod (c, [f,g]).

xod (d, [t1,t2]).

xod (e, [t3,t4]).

xod (f, [t5,t6]).

xod (g, [t7,t8]).

xod_max (a).

xod_max (d).

xod_max (e).

xod_max (f).

xod_max (g).

xod_min (b).

xod_min (c).

xod_min (t1).

xod_min (t2).

xod_min (t3).

xod_min (t4).

xod_min (t5).

xod_min (t6).

xod_min (t7).

xod_min (t8).

oc_term (a,4).

oc_term (b,4).

oc_term (c,1).

oc_term (d,4).

oc_term (e,6).

oc_term (f,2).

oc_term (g,1).

oc_term (t1,1).

oc_term (t2,4).

oc_term (t3,5).

oc_term (t4,6).

oc_term (t5,2).

oc_term (t6,1).

oc_term (t7,1).

oc_term (t8,1).

minmax (Poz, BestPoz, Oc):-

xod (Poz, SpPoz),!,

best(SpPoz, BestPoz, Oc);

oc_term(Poz, Oc).

best ([Poz], Poz, Oc):- minmax (Poz, _, Oc),!.

best ([Poz1| T], BestPoz, BestOc):-

minmax (Poz1, _, Oc1),

best (T, Poz2, Oc2),

vibor(Poz1,Oc1,Poz2,Oc2,BestPoz,BestOc).

vibor(Poz0, Oc0, Poz1, Oc1, Poz0, Oc0):-

xod_min (Poz0), Oc0>Oc1,!;

xod_max (Poz0), Oc0<Oc1,!.

vibor(Poz0, Oc0, Poz1, Oc1, Poz1, Oc1).

goal

minmax(a,BestPoz,Oc),write(BestPoz),write(Oc).

Дата добавления: 2015-06-27