Общие указания. Изменение давления dp с высотой в элементарном слое атмосферы толщиной dz описывается уравнением статики:

ГРАДИЕНТНЫЙ ВЕТЕР И ЕГО ИЗМЕНЕНИЯ С ВЫСОТОЙ

Лабораторная работа № 8

Изменение давления dp с высотой в элементарном слое атмосферы толщиной dz описывается уравнением статики:

dp = - r gdz (1)

где r - плотность воздуха в этом слое, g - ускорение свободного падения.

Интегрирование обеих частей этого уравнения от уровня моря до уровня z дает барометрическую формулу, согласно которой давление убывает с высотой по экспоненте. Скорость этого убывания зависит от средней виртуальной температуры слоя воздуха 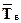и ускорения g:

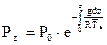(2)

где R - удельная газовая постоянная сухого воздуха равная 287 Дж/кгК. 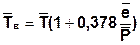, где 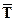- средняя температура воздуха, 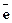- среднее парциальное давление водяного пара, 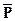- среднее давление в слое от земли до z.

Логарифмически дифференцируя(2), получаем:

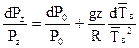(3)

Анализ уравнения (3) показывает, что изменение давления на уровне z (dP_z) определяется изменением давления у земли dP₀ иизменением средней виртуальной температуры d 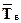причем, прямо пропорционально.

При d 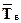= 0 dP_z по абсолютной величине в 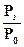раз меньше dP₀. В свою очередь dP₀ в 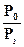раз больше dP_z и обратно зави­сит от изменения температуры: т.е. если d 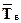> 0, то dP₀ < 0 и на­оборот. Следовательно с ростом 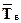давление у земли уменьшается, а на высоте увеличивается. При уменьшении 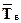давление у земли увеличивается, а на высоте уменьшается.

Атмосферное давление меняется не только по вертикали, но и по горизонтали. Изменение давления в пространстве удобно характеризо­вать вектором барического градиента 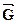, который имеет вертикаль­ную и горизонтальную составляющую G_z и G_n.

Вертикальный барический градиент 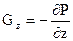из уравнения статики равен:

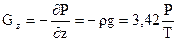(гПа/100м) (4)

В системе СИ G_z и G_n выражается в IIa/м.

Горизонтальный барический градиент представляет собой изменение давления по нормали к изобаре на горизонтальной плоскости:

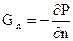(5)

На практике G_n выражают в гПа на градус меридиана, т.е. на 100км (гПа /100км). Зная величину вертикальной и горизонтальной составляющих барического градиента, можно найти угол наклона b изобари­ческих поверхностей к горизонтальной плоскости.

tgb = 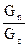(6)

т.е. b увеличивается с увеличением горизонтального барического гра­диента.

Градиентный ветер

Движение воздуха возникает при наличии перепада давления т.е. горизонтального барического градиента. Поскольку это движение возника­ет в атмосфере вращающейся Земли, тооноподвергается воздействию силы Кориолиса, силы трения, которая тормозит движение и меняет его направление, и центробежной силы, если изобары криволиней­ные.

Рассмотрим идеализированный случай ветра без трения. Такой ветер называется градиентным. При прямолинейных изобарах установившееся движение определяется только силой горизонтальногоградиента давления и силой Кориолиса. Такой ветер на­зывают геострофическим. Он дует вдоль изобар: в северном полушарии вправо от градиента давления G_n, в южном - влево, так, чтобы си­ла Кориолиса и сила градиента давления уравновешивали друг друга. Сила Кориолиса К = 2wc sinj, где с - скорость ветра. Поэтому по величине скорость геострофического ветра определяется выражением:

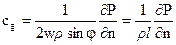(7)

где w - угловая скорость вращения Земли (w = 7,3 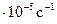), r - плотность воздуха (r = 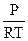), j - широта места, l = 2w sinj.

При круговых изобарах установившееся движение без трения называется геоциклострофическим или циклострофическим ветром. Он дует по касательной к изобарам. В северном полушарии в антициклоне oн направ­лен по часовой стрелке, в циклоне – против часовой стрелки. В южном полушарии – наоборот.

Для расчета скорости циклострофического ветра c_gc в циклоне используется формула:

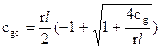(8)

а в антициклоне:

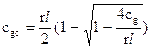(9)

Здесь r - расстояние от центра кривизны циклона или антициклона до данного пункта.

Формулы (8) и (9) удобны для расчетов в системе СИ.

Реальный ветер

В случае градиентного ветра не учитывается действие турбулентного и молекулярного трения. Это справедливо выше пограничного слоя, т.е. в свободной атмосфере ветер близок к градиентному по величине и направ­лению. В пограничном слое атмосферы, особенно в его нижней части - приземном слое (0 – 100м), влиянием трения пренебрегать нельзя. Си­ла трения уменьшает величину скорости ветра и отклоняет направление скорости ветра от изобары в сторону горизонтального градиента давле­ния G_n на угол a (от 15° до 35°), который дополняет угол между скоростью реального ветра c и G_n (j) до 90°. Т.е. a + j = 90° и a = 90° - j; j = 90° - a.

С учетом того, что сила трения R 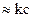при прямолинейных изо­барах угол j определяется выражением:

tgj = 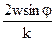(10)

где k - коэффициент трения.

В случае круговых изобар в циклоне:

tgj = 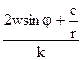(11)

в антициклоне:

tgj = 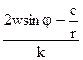(12)

где с - скорость реального ветра.

Из формул (10 – 12) видно, что чем больше трение (k), тем меньше угол j и больше угол a и наоборот. С увеличением широты угол j увеличивается, а угол a уменьшается.

Изменение скорости ветра с высотой в свободной атмосфере

В свободной атмосфере (выше 1 – 1,5км) ветер можно считать геострофическим. Его величина и направление зависят от величины и направления горизонтального барического градиента, которые могут изменяться с высотой под влиянием неоднородности распределе­ния температуры воздуха в горизонтальном направлении, т.е. от ве­личины и направления горизонтального градиента температуры Г.

Если взять слой воздуха толщиной Dz, то под действием горизонтального градиента средней виртуальной температуры в этом слое Г_m скорость геострофического ветра изменится, на величину Dс_g, называемую скоростью термического ветра с_т. Т.е.:

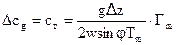(13)

Или, если выражать Dz в метрах, Г_m в °/100км, Т_m - в К, то:

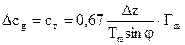(м/с) (14)

Есл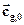и и 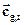- векторы скорости геострофического ветра на нижней и верхней границе слоя, а 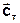- вектор скорости терми­ческого ветра, то изменение геострофического ветра с высотой опреде­ляется формулой (15), т.е. правилом параллелограмма:

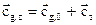(15)

Задание 1

Рассчитать скорость геострофического ветра на уровне 900гПа на широте j, если температура t, расстояние между изобарами Dn.

Варианты исходных данных:

Вар.
j, °
t, С	-25	-20	-15	-10
Dn, км

Задание 2

Рассчитать скорость геоциклострофического ветра в циклоне и антициклоне для тех же условий, которые даны в задании 1, если рассто­яние от циклона и антициклона составляет 800км.

Задание 3

Изобары направлены с севера на юг, давление убывает с запада на восток, изотермы направлены с запада на восток, температура убыва­ет с севера на юг, горизонтальный термический градиент Г = 3°/100км, горизонтальный барический градиент G_n = 2гПа/111км. Определить скорость и направление ветра на верхней, границе погранич­ного слоя, считая её равной 1,5 км, и на высоте 2км. Температура воздуха и давление на его нижней границе равны соответственно 5°С и 850 гПа, вертикальный градиент температуры равен 1°/100м. Широта пункта - 43°с.ш.

Контрольные вопросы

1.В каком соотношении находятся скорости градиентного ветра при одном и том же градиенте давления при прямолинейных изобарах в циклоне, в антициклоне?

2.Как связано изменение направления ветра с высотой с адвекцией тепла и холода в свободной атмосфере?

Дата добавления: 2015-06-28