Со скольжением в трубе от числа при разных значениях числа Маха

.

Где

Имея и виду, что

Подставим в (27), а также на основании (5) значение

Где - полная длина трубы. В этом решении один корень отброшен (с отрицательным знаком) как не отвечающий физическим условиям задачи (при). Если вычитаемое под корнем значительно меньше единицы, то справедливо приближенное решение, позволяющее определить падение давления в трубе без учета сжимаемости газа

Отсюда следует

Которое после интегрирования с учетом граничного условия

Значение коэффициента трения в начале трубы. Используя уравнение состсяния для идеального газа, из (26) получаем дифференциальное уравнение

Где

при

и некоторых элементарных преобразований дает (при )

(27)

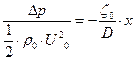. (28)

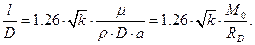
получим при

(29)

Решение (28) справедливо лишь при . Зависимость коэффициента трения от числа Рейнольдса при различных значениях числа Маха представлена на рис. 4.

Рис. 4. Зависимость коэффициента трения при течении

Дата добавления: 2015-06-28