Проверка устойчивости плоской формы деформирования рамы

Проверка производится по формуле (33) [5]

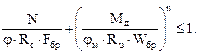
Поскольку угол между стойкой и ригелем рамы 90º+16,7º= =106,7º< 130º, расчетную длину ригеля и стойки в соответствии с п.6.29 [5] следует принимать равной длинам их внешних подкрепленных кромок, т.е. для стойки l_р.ст = Н = 3,25 м, а для ригеля

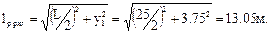
Суммарная расчетная длина по наружной кромке рамы

l_р.нар = 3,25 + 13,05 = 16,3 см.

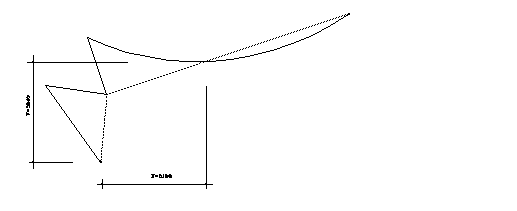
Рис. 15. Эпюра изгибающих моментов

Расчетная схема полурамы и эпюра моментов в прямолинейном элементе показаны на рис. 15.

Находим координаты точки перегиба эпюры моментов, для этого приравниваем к нулю уравнение моментов в сечении 1-1:

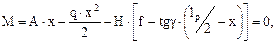
где ;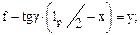

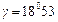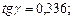
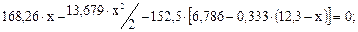
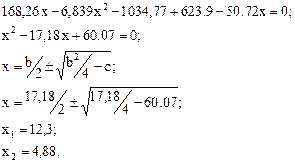
Точка перегиба находится на расстоянии х < 0,5L, этому условию удовлетворяет корень х = 4,88;

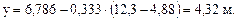
Расчетная длина рамы по наружной кромке имеет два участка, первый 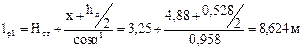, где имеются закрепления по растянутой зоне (по ригелю – прогонами или плитами, по стойке – стеновыми панелями) и второй 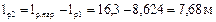, где нет закреплений растянутой зоны.

Расчет устойчивости плоской формы деформирования производим по формуле

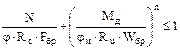(10)

для первого участка с показателем n=1 и для второго участка с показателем n=2.

Проверка устойчивости плоской формы деформирования рамы проводится на двух участках l_р1 и l_р2:

1. Для участка l_р1 = 8,624 м гибкость из плоскости рамы

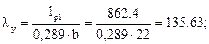
коэффициент продольного изгиба

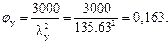
Коэффициент j_м определяем по формуле (23) [5]:

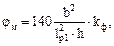
где k_ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l_р1, определяемый по табл. 2 прил. 4 [5]. Для нашего случая имеем

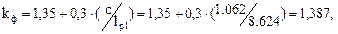
где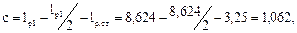

здесь l_р1 = Н_ст = 3,25 м;

тогда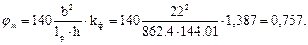

Ригель раскреплен по растянутой кромке, поэтому коэффициенты j_у и j_м, соответственно, следует умножать на коэффициенты К_пn и К_пм.

Определяем коэффициенты:

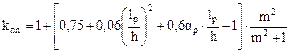(формула (34) из [5].

Для прямолинейного участка ригеля a_р = 0, а отношение 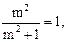так как число закреплений m > 4, тогда

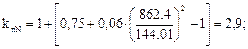
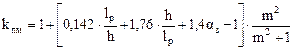(формула 24);

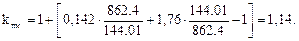
Подставляем полученные значения в формулу

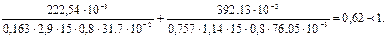
Устойчивость плоской формы деформирования обеспечена.

2. Для участка l_р2 = 7,68 м расчетная длина по осевой линии

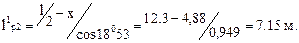
Определяем максимальную высоту сечения ригеля на данном участке:

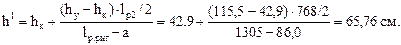
Подсчитываем максимальный момент и продольную силу в сече-

нии с координатами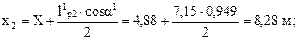

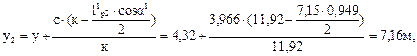
где с и к подсчитаны выше.

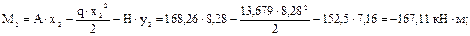
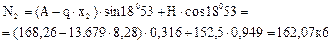
Для определения величины момента по деформируемой схеме определяем площадь и момент инерции сечения:

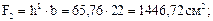
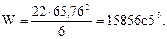
По интерполяции получим значения коэффициента m_б для h¹ = 65,76 см. по табл. 7 [5]:

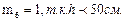
Для учета переменной высоты сечения находим по табл. 1 прил. 4 [5]:

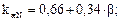
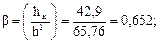
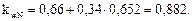
Определяем гибкость:

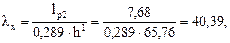
тогда 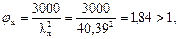так как 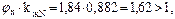принимаем j_х×k_жN = 1.

где N – продольная сила в коньковом сечении (ключевом шарнире); N = 144,7 кН.

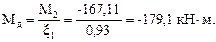
Гибкость из плоскости рамы

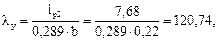
тогда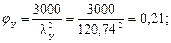

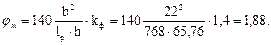
При расчете элементов переменного по высоте сечения, не имеющих закреплений из плоскости по растянутой от момента кромки, при расчете устойчивости плоской формы деформирования, коэффициенты j_у и φ_м следует умножать на коэффициенты К_жN и К_жм по табл. 1 и 2 прил. 4 [5]:

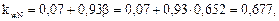
где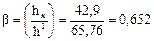

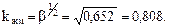
Подставляем полученные значения в формулу проверки устойчивости плоской формы деформирования:

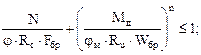
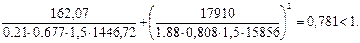
Устойчивость плоской формы деформирования на втором участке обеспечена.

Дата добавления: 2015-06-28