Примеры построения третьего вида некоторых геометрических тел

В заданиях при построении третьего вида предмета по двум данным сначала необходимо представить его форму в целом. Форма многих предметов усложнена различными вырезами, скосами и выступами. Вначале надо определить поверхности, которыми ограничен предмет, и их расположение, а затем положение точек и линий на этих поверхностях.

Если предмет имеет плоскости симметрии, то их принимают за базовые для отсчета соответствующих размеров.

На рисунке 2.3 показано построение вида слева шестигранной правильной призмы со сквозным отверстием. Призма имеет две плоскости симметрии. Для показа последовательности построений использована постоянная прямая чертежа.

На рисунке 2.4 изображена четырехугольная усеченная пирамида с вырезом двумя плоскостями.

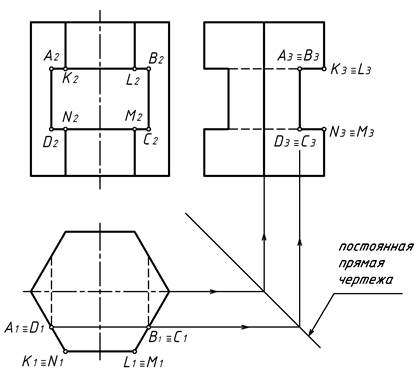
Рисунок 2.3 – построение трех видов шестигранной призмы

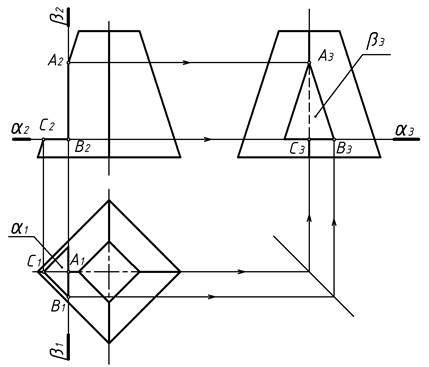
Рисунок 2.4 – построение трех видов усеченной пирамиды

На рисунках 2.5, 2.6, 2.7 показано построение третьего вида предмета, ограниченного поверхностями вращения, с различными вырезами. При этом показано, что третий вид можно строить и без постоянной прямой чертежа, используя координаты y.

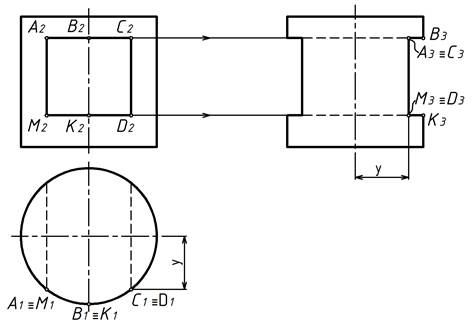
Рисунок 2.5 – построение трех видов цилиндра

Рисунок 2.6 – построение трех видов конуса

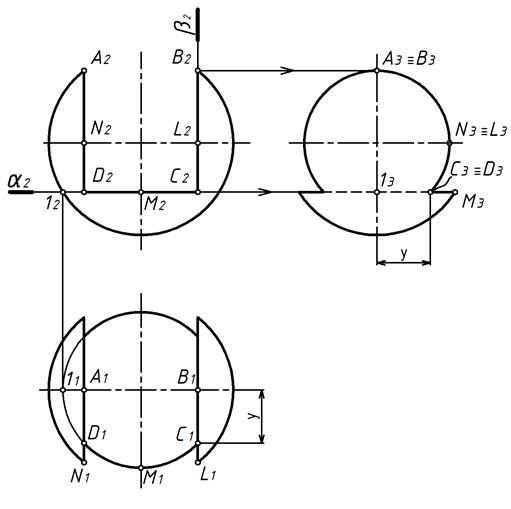
Рисунок 2.7 – построение трех видов сферы

2.3. Примеры построения натуральной величины наклонного сечения

Сечение – изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями.

Наклонное сечение - сечение предмета плоскостью, перпендикулярной к одной из плоскостей проекций. На эту плоскость проекций секущая плоскость проецируется в виде линии, называемой следом плоскости. Наклонная секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого. Поэтому сечение на эту плоскость проецируется с искажением.

Чтобы получить натуральный вид сечения, его надо проецировать на дополнительную плоскость проекций, параллельную следу секущей плоскости.

Любой предмет можно условно разбить на составляющие его геометрические тела.

Рассмотрим построение натуральной величины сечения призмы наклонной плоскостью α, перпендикулярной фронтальной плоскости проекций (рисунок 2.8). Построение начинают с проведения линии, параллельной следу плоскости, от которой ведут построение фигуры сечения (в нашем случае это линия x2,4). Чтение формы наклонного сечения упрощается, если построить горизонтальную проекцию наклонного сечения, как наложенное сечение.

Построение точек сечения производят, откладывая размеры a и в, взятые с горизонтальной проекции призмы и размера ℓ, взятого с фронтальной проекции призмы.

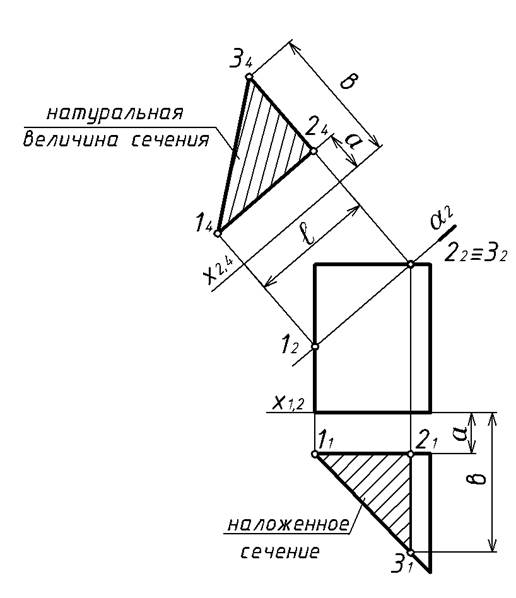
Рисунок 2.8 – построение натуральной величины сечения

На чертеже след секущей плоскости задают в виде разомкнутой линии со стрелками, указывающими направление взгляда, и одинаковыми прописными буквами русского алфавита (рисунок 2.9). Сечение необходимо заштриховать.

Построение натуральной величины сечения можно упростить, если в качестве линии отсчета взять другую прямую, например, 11-21 (рисунок 2.9)или линию симметрии детали (рисунок 2.10), если она имеется.

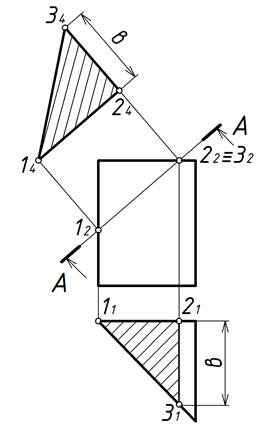
Рисунок 2.9 – построение натуральной величины сечения призмы

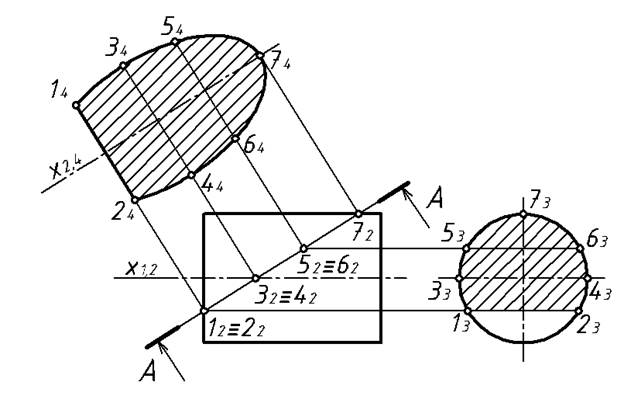
Рисунок 2.10 – построение натуральной величины сечения цилиндра

На рисунке 2.10 показано построение натуральной величины сечения цилиндра наклонной плоскостью А-А.

Плоскость А-А пересекает цилиндрическую поверхность по эллипсу. Эллипс является симметричной фигурой, поэтому за линию отсчета можно принять его ось симметрии. Эллипс строят как лекальную кривую. Количество промежуточных точек произвольное.

На рисунке 2.11 представлено построение натуральной величины сечения сферы плоскостью А-А. Сфера сечется плоскостью по окружности. На вид сверху эта окружность проецируется эллипсом.

При проецировании на плоскость, параллельную секущей плоскости А-А сечение представится в виде окружности. Центр окружности находится в точке пересечения перпендикуляра, опущенного из центра сферы О2 на плоскость

А-А(точка С2), а радиус этой окружности равен отрезку С2-К2, где К2 – точка пересечения очерка сферы со следом секущей плоскости А-А.

Рисунок 2.11 – построение натуральной величины сечения сферы

Дата добавления: 2015-06-28