Внутренние силовые факторы

Теперь

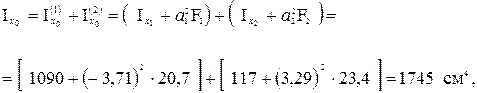
4. Определяем величины главных моментов инерции

Таким образом, получим I₁=I_max=1754 см⁴, I₂=I_min=859 см⁴.

5. Определяем положение главных центральных осей OX₀ и OY₀:

a₁= arctg(– 0,1003) = – 5,27= 5,78°,

a₂= arctg(9,8773) = 80,73= 84,22°.

Положение главных центральных осей OX₀ и OY₀ показано на рис. 1.14.

6. Проверка правильности решения.

а) в данном примере

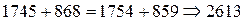см⁴ ;

б) в данном примере

1745×868 – (– 89,7) ² = 1754×859 – 0;

в) tga₁×tga₂ = – 1, в данном примере

tg(– 5,78°)×tg(84,22°) = – 0.1003 × 9,8773» – 1.

[В.В.,В.Н1]

2.1 Понятия упругости и пластичности

Опыты показывают, что под действием внешних нагрузок размеры и форма тела всегда изменяются, даже при малой величине нагрузки. Это явление называют деформацией.

При относительно малых нагрузках деформация исчезает после удаления вызвавшей ее нагрузки; такая деформация называется упругой. Способность тела восстанавливать свои размеры и форму после удаления нагрузки называют упругостью.

При больших нагрузках часть деформации не исчезает после удаления вызывающей ее нагрузки. Деформация, сохраняющаяся после удаления вызывающей ее нагрузки, называется остаточной или пластической. Способность материала воспринимать пластические деформации без разрушения называют пластичностью.

2.2 Основные допущения о свойствах деформируемых тел

При изучении поведения тел под действием внешних нагрузок, обычно производится схематизация рассматриваемых тел; учет всех реальных свойств невозможен. Например, теоретическая механика оперирует с абсолютно твердым телом, в то время как все реальные тела под действием внешних нагрузок деформируются. Деформируемым телам приписывают следующие основные свойства.

1. Непрерывность. Представим объем, занимаемый телом, заполненным веществом сплошь, без разрывов, т.е. не будем учитывать реальное строение тел из атомов.

При такой схематизации твердого тела нужно отказаться от вычисления сил взаимодействия между отдельными атомами вещества. Вместо этого необходимо рассматривать равнодействующие большого числа межатомных сил, действующих по какой-либо площадке, называя их внутренними силами.

Принятое допущение позволяет применять к исследованию деформации твердых тел методы анализа бесконечно малых величин.

2. Идеальная упругость. Принимается, что деформируемое тело испытывает только упругие деформации, являющиеся однозначной функцией нагрузок. В реальных телах наблюдаются некоторые неупругие явления (например, местные микроскопические пластические деформации), однако в большинстве случаев эффект их мал и его можно не учитывать.

3. Изотропность, т.е. одинаковость свойств по различным направлениям.

4. Однородность.

2.3 Расчетные схемы

Для расчета стержня составляют его расчетную схему, в которой показывают форму оси стержня, типы опор и внешние нагрузки, действующие на стержень.

По форме оси различают стержни с прямой, кривой и ломаной осью.

В процессе нагружения стержней их поперечные сечения получают перемещения, т.е. их положение в пространстве изменяется. Поворот поперечного сечения называют угловым перемещением, изменение положения центра тяжести - линейным перемещением.

Поперечные сечения стержня получают перемещения в результате движения стержня как жесткого тела (в этом случае перемещения всех поперечных сечений одинаковы) и деформации стержня. В последнем случае каждое поперечное сечение перемещается относительно других поперечных сечений.

Чтобы устранить движение стержня как жесткого тела, применяются устройства, называемые опорами и запрещающие перемещения некоторых сечений. Поперечное сечение, перемещения которого ограничены опорой, называют опорным сечением.

Наиболее часто встречаются следующие типы опор.

1. Шарнирно-подвижная, запрещающая одно линейное перемещение опорного сечения.

2. Шарнирно-неподвижная, запрещающая линейное перемещение опорного сечения в двух взаимно перпендикулярных направлениях (например, по вертикали и по горизонтали).

3. Защемляющая опора, запрещающая как линейные, так и угловые перемещения опорного сечения.

Изображения этих опор в расчетных схемах стержней показаны на рис. 2.1.

Внешними называют нагрузки, действующие на данное тело со стороны других тел. Существуют два типа внешних нагрузок: объемные и поверхностные. Объемными называют нагрузки, приложенные ко всем частицам объема тела (например, давление газа или жидкости на стенки сосуда, давление одной детали на другую по поверхности контакта).

В расчетных схемах стержней удобно относить нагрузки (как объемные, так и поверхностные) к единице длины стержня. Такие нагрузки называют погонными.

Погонные нагрузки характеризуются их интенсивностью - величиной нагрузки на единицу длины стержня. Размерность интенсивности погонной нагрузки - единица силы, поделенная на единицу длины. Интенсивность погонной нагрузки будем обозначать буквой q, в случае необходимости указывая индексом, какой оси параллельна погонная нагрузка.

Рис. 2.1

Если длина площадки, по которой распределена погонная нагрузка, мала по сравнению с длиной стержня, нагрузку считают сосредоточенной в одной точке. Такие нагрузки называют сосредоточенными силами.

При составлении расчетной схемы стержня каждую нагрузку приводят к центру тяжести того поперечного сечения, в плоскости которого приложена эта сила.

Если к центру тяжести поперечного сечения приводится сосредоточенная сила, то в расчетной схеме стержня получим в общем случае силу и пару сил. Эту пару называют сосредоточенным моментом. Размерность сосредоточенного момента - единица силы, умноженная на единицу длины.

Если к центрам тяжести поперечных сечений приводится погонная нагрузка, то в расчетной схеме стержня получим погонную силовую и погонную моментную нагрузки. Погонная моментная нагрузка характеризуется ее интенсивностью - величиной момента на единицу длины стержня. Размерность интенсивности погонной моментной нагрузки - единица силы.

Изображение различных типов нагрузок в расчетных схемах стержней показано на рис. 2.2.

Рис. 2.2

2.4 Внутренние силовые факторы в поперечных сечениях стержней

Рассмотрим стержень, на который действует уравновешенная система сил (рис. 2.3).

Рис. 2.3

Мысленно рассечем стержень плоскостью по некоторому поперечному сечению А и рассмотрим одну из полученных частей стержня, например левую (Рис.2.4).

Рис. 2.4

Она находится в равновесии под действием внешних сил, приложенных к этой части стержня, и внутренних сил, действующих со стороны отброшенной части стержня на оставленную для рассмотрения.

Для составления уравнений равновесия выберем прямоугольную систему координат X, Y, Z, связанную с рассматриваемым поперечным сечением. Начало координат поместим в центр тяжести сечения. Ось Z будем направлять по продольной оси стержня, по внешней нормали к сечению. За оси X и Y примем главные центральные оси инерции рассматриваемого сечения. Положительные направления осей X, Y, Z выберем так, как показано на рис. 2.5.

Рис. 2.5

Обозначим главный вектор внутренних сил в данном поперечном сечении стержня , а их главный момент относительно центра .

Проекции главного вектора внутренних сил и проекция главного момента внутренних сил на оси X, Y, Z называют внутренними силовыми факторами (ВСФ) в данном поперечном сечении стержня.

Для ВСФ приняты следующие наименования:

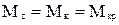- поперечные силы, - продольная сила; (или ) - изгибающие моменты, - крутящий момент.

2.5 Уравнения внутренних силовых факторов

В общем случае ВСФ изменяются по длине стержня, т.е. в разных сечениях они могут иметь различную величину. Чтобы составить уравнения, показывающие как зависит ВСФ от положения сечения, необходимо выполнить следующие операции.

1. Определить, на сколько участков делится стержень внешними нагрузками.

Участком называется часть стержня, на протяжении которой к стержню не приложены сосредоточенные нагрузки, а интенсивность погонной нагрузки может быть задана аналитически одним уравнением. Границами участков являются концевые сечения стержня, сечения, в которых приложены сосредоточенные нагрузки, в которых скачками изменяется интенсивность погонной нагрузки, и те сечения, в которых изменяется характер зависимости интенсивности погонной нагрузки от абсциссы сечения. Например, стержень (рис. 2.6) делится приложенными нагрузками на семь участков.

Рис. 2.6

2. Задать положение произвольного сечения рассматриваемого участка. Указать положение произвольного сечения участка в выбранной системе координат нельзя, так как ее начало как раз находится в центре тяжести этого произвольного сечения.

3. Положение произвольного сечения данного участка задают его абсциссой u. Ось абсцисс U направляют по оси стержня. Положительное направление оси U совпадает с положительным направлением оси Z.

Начало отсчета на оси U совмещают с одной из границ участков, имеющихся на оставленной для рассмотрения части стержня. Для каждого участка, составляя уравнения ВСФ, будем указывать с помощью индекса, соответствующего номеру участка, абсциссы произвольного сечения участка: - абсцисса произвольного сечения i - го участка.

В зависимости от того, где выбрано начало отсчета , пределы изменения для данного участка будут различными. При составлении уравнений ВСФ необходимо указывать пределы изменения абсцисс произвольного сечения рассматриваемого участка при выбранном начале отсчета.

4. Определить ВСФ в произвольном сечении рассматриваемого участка.

В результате этой операции ВСФ будут выражены как функции . Удобно обозначить эти функции и т.д. В ряде случаев абсциссу «u» обозначают буквой z. Тогда функции сил и моментов обозначают как и т.п.

Имея эти функции, можно определить численные значения ВСФ в любом поперечном сечении стержня. Для этого необходимо в уравнение ВСФ того участка, которому принадлежит рассматриваемое сечение, подставить численное значение абсциссы данного сечения.

2.6. Графики (эпюры) внутренних силовых факторов

В общем случае ВСФ являются функциями абсциссы сечения. Графики этих функций называют эпюрами ВСФ.

Эпюры ВСФ располагают под схемами стержней. За ось эпюры принимается линия, копирующая ось стержня. Принято штриховать эпюры прямыми линиями, перпендикулярными оси эпюры, и указывать знак ВСФ в соответствии с принятым правилом знаков. Длина штриховочных линий в принятом для построения масштабе изображает величину внутреннего силового фактора в том сечении, против которого проводится эта линия.

Масштаб построения эпюр обычно не указывают; вместо этого непосредственно указывают значение ВСФ, изображаемых ординатами эпюр на границах участков и в тех сечениях, в которых ВСФ имеют экстремумы. Для тех ВСФ, которые во всех сечениях равные нулю эпюры не строят.

2.7 Дифференциальные зависимости между ВСФ и внешними нагрузками

Рассмотрим элемент стержня, т.е. часть стержня, ограниченную двумя бесконечно близкими сечениями (рис. 2.7).

Рис. 2.7

Внутренние силы в правом концевом сечении элемента могут отличаться от внутренних сил в левом концевом сечении только на бесконечно малую величину.

Составим уравнения равновесия элемента стержня:

откуда

.

Проектируя это уравнение на оси координат, получим следующие дифференциальные зависимости между ВСФ и внешними нагрузками:

.

Из остальных уравнений равновесия элемента стержня получим аналогичные зависимости для моментов

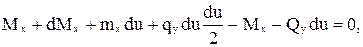
откуда

В частном случае, когда , .

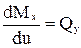Аналогично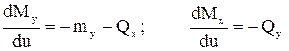

Производная от какого-нибудь внутреннего силового фактора по абсциссе сечения равна тангенсу угла между касательной к эпюре этого внутреннего силового фактора и осью абсцисс. Поэтому, пользуясь дифференциальными зависимостями между внутренними силовыми факторами и внешними нагрузками, можно проверять правильность построения эпюр ВСФ.

Следует также учесть, что если в каком-нибудь сечении стержня приложена сосредоточенная нагрузка, то на эпюре ВСФ в этом сечении имеется разрыв на величину сосредоточенной нагрузки: в сечениях, где приложена сосредоточенная сила имеется разрыв на эпюре сил (того же индекса) на величину сосредоточенной силы; в сечениях, где приложен сосредоточенный момент, имеется разрыв на эпюре моментов (того же индекса) на величину сосредоточенного момента.

Наоборот, если в данном сечении нет сосредоточенной нагрузки, на эпюрах ВСФ не может быть разрыва в этом сечении

2.8. Алгоритм определения ВСФ

1. Разложить заданные нагрузки по направлениям оси стержня и главных центральных осей инерции поперечных сечений.

2. Определить реакции опорных связей.

3. Определить, на сколько участков делится стержень приложенными к нему внешними нагрузками.

Необходимо помнить, что границами участков являются концевые сечения и те сечения, в которых приложены сосредоточенные нагрузки (включая реакции опор) или изменяется уравнение интенсивности погонной нагрузки.

Уравнения ВСФ составляются отдельно для каждого участка.

4. Мысленно рассечь стержень по произвольному (не совпадающему ни с одной из границ участка) сечению рассматриваемого участка. Произвольное сечение участка делит стержень на две части (независимо от числа участков).

5. Выбрать для рассмотрения одну из двух частей стержня. Рекомендуется рассматривать ту часть стержня, на которую действует меньше нагрузок.

6. Выбрать начало отсчета абсцисс поперечных сечений рассматриваемого участка.

7. Определить пределы изменения абсцисс поперечных сечений рассматриваемого участка при выбранном начале отсчета. Разность пределов равна длине участка.

8. В произвольном сечении рассматриваемого участка провести оси координат.

Ось Z направляется по продольной оси стержня по внешней нормали к сечению. Оси X и Y направляются по главным центральным осям инерции поперечного сечения.

9. Составить уравнения ВСФ для рассматриваемого участка.

10. Составить уравнения ВСФ для всех участков стержня.

11. Определить численные значения ВСФ на границах участков и в тех сечениях, где ВСФ имеют экстремальные значения (минимум или максимум).

12. По составленным уравнениям построить графики (эпюры) ВСФ. Для каждого ВСФ строится отдельный график (эпюра). Ось эпюры копирует ось стержня. На нормалях к оси эпюры откладываются отрезки, изображающие в принятом для построения масштабе величину ВСФ в тех сечениях, где проведены эти отрезки. Концы отрезков соединяются кривой, соответствующей уравнению данного ВСФ. Указать величину ВСФ на границах участков и экстремумы.

13. Произвести контроль построенных эпюр.

В том сечении, в котором к стержню приложена сосредоточенная сила, соответствующая эпюра сил имеет разрыв на величину силы. В других сечениях на эпюре сил разрывов нет. В том сечении, в котором к стержню приложен сосредоточенный момент, соответствующая эпюра моментов имеет разрыв на величину момента. В других сечениях на эпюре моментов разрывов нет.

Наклон касательных к эпюре ВСФ определяется дифференциальными зависимостями между ВСФ и внешними нагрузками.

Использование предлагаемого метода сечений для отыскания ВСФ имеет принципиальное ограничение. Если число связей, налагаемых опорами таково, что уравнений статики недостаточно для отыскания реакций опор, то метод сечений не пригоден. В этом случае используют методы раскрытия статической неопределимости, достаточно громоздкие в реализации. Ниже будет показано, как устранить такие трудности, используя решения, основанные на анализе общих математических моделей деформирования.

Для закрепления знаний по вычислению ВСФ в прил.2 приведены варианты индивидуальных заданий.

Дата добавления: 2015-06-28