Дисконтирование по сложной ставке

Определение срока ссуды и величины процентной ставки

Так же как для простых процентов, для сложных процентов необходимо иметь формулы, позволяющие определить недостающие параметры финансовой операции:

-срок ссуды: n = [log (S / P)] / [log (1 + i)] = [log (S / P) ] / (log(1 + j / m) ^m);

-ставка сложных процентов: i= 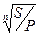-1

Пример 6. Что выгоднее: увеличение вклада в три раза за три года или 46% годовых?

Решение:

Такого рода задачи приходится решать не только лицам, занимающимся финансовой работой, но и населению, когда решается вопрос о том, куда выгоднее вложить деньги. В таких случаях решение сводится к определению процентной ставки:

Таким образом, увеличение вклада за три года в три раза эквивалентно годовой процентной ставке в 44,3%, поэтому размещение денег под 46% годовых будет более выгодно.

I= 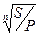-1= - 1= 0,443

Первое заключается в определение первоначальной сумме Р по значению наращенной суммы S при заданной ставке процента, второе - при заданной учетной ставке. Дисконтируя сумму S по сложной ставке процентов, получим

P = S / (1+i)ⁿ = Svⁿ ,

Vⁿ = (1+i)^-n = 1/qⁿ

Величину vⁿ называют дисконтным, учетным,или дисконтирующим, множителем.

Для случаев, когда проценты начисляются m раз в году, получим

P = S / (1+j/m)^mn = Sv^mn,

V^{mn =} (1+j/m)^-mn

Величину Р, полученную дисконтированием S, называют современной, текущей, стоимостной, или современной величиной S. Современная стоимость может быть рассчитана на любой срок до выплаты S.

Разность S – Р, в случае, когда Р определенно дисконтированием, называют дисконтом. Обозначим последний через D:

D = S – P = S (1-vⁿ).

Дата добавления: 2015-06-28