Булеві формули і пріоритет операцій

Мінімізація булевих функцій

Лекція 10

Порядок выполнения

1. Ослабив винт 2 (рис.3), установите плоскость под углом 0^° к горизонту. Поместите брусок 4 (алюминий-дерево) на наклонную плоскость в положении деревом вниз.

2. Переключите тумблер управления электромагнитами механического блока в положение

«плоскость».

3. Переведите секундомер СЭ1 в режим 1.

4. Нажмите кнопку «Пуск» секундомера. Измерьте время опускания груза.

5. Повторите опыт не менее 5 раз. Определить абсолютную и относительную погрешность полученных результатов.

6. Найдите ускорение бруска по формуле (6) и коэффициент трения по формуле (7). Сравните полученный в опыте результат с табличным значением коэффициента трения

скольжения.

7. Меняя угол наклона плоскости, найдите ускорение бруска по формуле (6).

8. Постройте зависимость a (α). Сравните полученный результат с теоретическим, найденным по формуле (9).

9. Повторите п.п. 1-8, повернув брусок в положение алюминием вниз.

10. Сделайте выводы.

Контрольные вопросы

1. Дайте определение силы, равнодействующей силы. Единица измерения силы.

2. Сформулируйте закон инерции. Что называется движением по инерции?

3. Какие системы отсчета являются инерциальными и неинерциальными. Приведите примеры.

4. Дайте определение массы тела. Укажите основные свойства масс.

5. Сформулируйте законы Ньютона.

6. Выведите расчетную формулу (7).

7. Выведите расчетную формулу (9).

Булеві функції можуть бути задані аналітично, тобто формулами.

Формула – це вираз, що містить булеві функції та їхні суперпозиції. Суперпозицією називають спосіб одержання нових функцій шляхом підстановки в одну функцію замість аргументу другу функцію.

Приклад. F(x, y, z) = (x ⋁ y̅) ∧ z; Якщо функція g(x₁) – заперечення, s(x₁, x₂) – кон’юнкція, p(x₁, x₂) – диз’юнкція, то F(x, y, z) = s(p(x, g(y)), z).

У формулі (x ⋁ y̅) ^ z використовується запис Infix, коли знаки операцій розташовані між операндами. Для запису виразів в інфіксній формі треба визначити порядок виконання логічних операцій, що визначається або присутністю дужок або пріоритетом операцій.

Якщо в виразі відсутні дужки, то операції будуть виконуватись в такій послідовності: інверсія, кон’юнкція, диз’юнкція, імплікація, еквівалентність.

Приклад. З урахуванням пріоритету операцій в виразі розставимо дужки:

x ~ z ® x̅ ⋁z = x ~ (z ® ((x̅) ⋁z).

Навпаки, в виразі треба усунути зайві дужки:

(((x ⋁ y) ∧z) ~(x̅) = (x ⋁ y) ∧z ~ x̅

Зверніть увагу, що операція інверсії (заперечення) може визначатись не тільки для окремих змінних, але й для цілого виразу: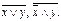

На відміну від табличного визначення функції зображення функції формулою не є однозначним. Наприклад, функцію штрих Шеффера можна зобразити за допомогою операцій булевої алгебри: 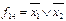, або , а функція стрілка Пірса 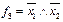, або .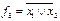

Формули, що зображують одну й ту ж функцію, називають еквівалентними або рівносильними.

Еквівалентність формул позначається знаком рівності. Один із способів встановити еквівалентність функцій – побудувати їх таблиці істинності, а потім порівняти рівність результатів для кожної інтерпретації.

Перевіримо еквівалентність функцій f₁ = x ⊕ (y∧z), f₂ = (x ⊕ y)∧ (x ⊕ z).

x	y	z	y∧z	f1		x ⊕ y	x ⊕ z	f2

При побудові таблиці істинності для аргументів будуємо всі можливі інтерпретації. Для цього вписуємо в кожен рядок інтерпретації двійкові коди натуральних чисел від 0 до 2ⁿ, де n – кількість аргументів. Для кожної операції виділяємо окремий стовпчик.

В результаті робимо висновок, результат не сходиться тільки в одній інтерпретації (0, 0, 1). Але цього досить, щоб зробити висновок: функції не еквіваленті f₁ ¹ f₂.

Дата добавления: 2015-06-28