Логічні схеми. 1. Дайте визначення суперпозиції булевої функції

Запитання

1. Дайте визначення суперпозиції булевої функції.

2. Який пріоритет мають операції алгебри логіки?

3. Яким чином будується таблиця істинності булевої функції?

4. Які формули називають еквівалентними?

Логічні схеми у комп’ютерах та інших електронних пристроях оперують з наборами вхідних та вихідних даних, що складаються з нулів і одиниць. Булева алгебра і булеві функції зображують математичний апарат для роботи з такими даними і використовуються для аналізу та синтезу логічних схем (ланцюгів). Основою побудови логічних схем є набір логічних елементів.

Таблиця 1 Основні логічні елементи

Назва	Символ логічних елементів	Булева функція
І		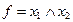Кон’юнкція
АБО		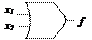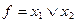Диз’юнкція
НЕ		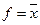Інверсія
І-НЕ		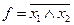штрих Шеффера
АБО-НЕ		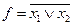Стрілка Пірса
ВИКЛЮЧНЕ АБО		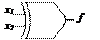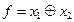ХОР

Кожний логічний елемент реалізує деяку логічну функцію. Його входи відповідають булевим змінним, а вихід – значення функції. Графічні символи і назви найчастіше використовуваних логічних елементів зображено в таблиці1.

Набір логічних елементів повний, якщо з його допомогою можна реалізувати будь-яку булеву функцію. Логічна схема будується з набору базових елементів і зображує суперпозицію даних елементів так само, як формула є суперпозицією базових функцій булевої алгебри.

Логічні елементи, що реалізують операції з властивостями асоціативності, на схемах можуть зображуватися з числом входів більше двох, що означає багаторазове застосування даної операції.

Наприклад, логічний елемент АБО може мати 3 входи:

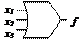
Приклад. Побудувати логічний ланцюг, що реалізує функцію f(x, y, z) = (x⋁y)∧z.

Під час дослідження логічних ланцюгів виникають дві основні задачі: аналіз і синтез. Аналіз логічного ланцюга полягає у побудові булевої функції, яка реалізує даний логічний пристрій. Для цього визначається значення вихідного сигналу на всіх наборах вхідних даних і складаємо таблицю істинності функції. Далі будуємо функцію, що еквівалентна даній функції, але містить тільки логічні операції, для яких є логічні елементи, що реалізують операцію, це може бути ДДНФ (досконала диз’юнктивна нормальна форма). Задача синтезу полягає в побудові логічного ланцюга для ДДНФ.

Для побудови ДДНФ побудуємо конституенти одиниці функції. Розглянемо процедуру на прикладі: f(x, y, z) = (x®y)~(y̅∧z).

x	y	z	x®y	y̅	y̅∧z	f

Конституенти будуємо для тих інтерпретацій, де f = 1. Будуємо їх як кон’юнкції змінних, виконуючи інверсію тих змінних, значення яких в даній інтерпретації – 0.

Тобто, для f(0, 0, 1) = 1, перша конституента має вигляд: x̅∧y̅∧z. Для f(1, 0, 0) = 1 друга конституента має вигляд: x∧y̅∧z̅.

ДДНФ f =(x̅∧y̅∧z)Ú(x∧y̅∧z̅).

Спростимо формулу, використовуючи закони булевої алгебри. Використаємо закон де Моргана: ДДНФ f =(x̅∧y̅∧z)Ú(x∧y̅∧z̅) = .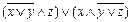

Перевіримо, чи еквівалентна побудована функція даній.

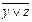
x	y	z			∧z	x ∧	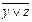f

Побудована ДДНФ еквівалентна даній функції, але містить тільки ті операції, для реалізації яких є відповідні логічні елементи.

Побудуємо логічну схему:

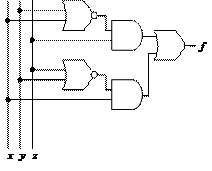
При побудові логічних схем з лівого краю накреслити вертикальні лінії – входи. Перший ряд елементів – операції вищого пріоритету, або ті, що в формулі взяті в дужки. З вертикальних провідників x, y, z сигнали на входи логічних елементів визначаємо горизонтальними лініями.

Точки контакту вертикальних і горизонтальних ліній виділяємо на малюнку. Далі другий ряд елементів визначається за рівнем пріоритету операцій.

Дата добавления: 2015-06-28