Гипербола

Эллипс

I Каноническое уравнение эллипса

Определение 1. Эллипсом называется линия, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

(1)

где a и b – некоторые положительные числа.

Уравнение (1) не изменится, если заменить x на (–x). Это означает, что вместе с точкой (x ₀, y ₀) эллипсу принадлежит и точка (– x ₀, y ₀), т.е. эллипс (1) симметричен относительно оси Oy. Аналогично, можно сделать вывод и о симметрии относительно оси Ox. Поэтому достаточно рассмотреть линию (1) лишь в первой четверти, где явное уравнение эллипса (1) имеет вид:

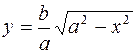. (2)

Функция (2) убывает от y (0)= b до y (a)=0, при x>a – не существует. Методами математического анализа можно показать, что линия (2) выпукла вверх и перпендикулярна осям координат в точках пересечения с ними.

II Определяющее свойство эллипса

Предположим, что a>b и обозначим 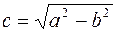. Точки F ₁(–c;0) и F ₂(c;0) называются фокусами эллипса (если b>a, то и фокусы лежат на Oy на расстоянии с от начала координат). Докажем, что для любой точки эллипса сумма ее расстояний до фокусов равна 2 а.

Пусть M (x, y) – произвольная точка эллипса (1). Тогда 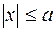, . Вычислим расстояние:

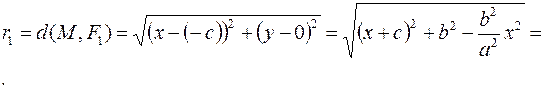
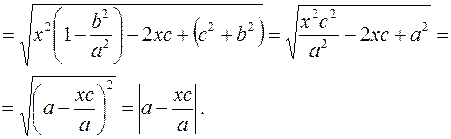
Так как с<a,то и , поэтому выражение под знаком модуля в формуле для r ₁ положительно. Значит

.

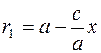Аналогично можно показать (покажите!), что

.

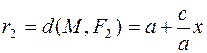Легко увидеть, что r ₁ +r ₂ = 2 a.

Доказанное свойство можно взять за определение эллипса, после чего получить каноническое уравнение (1) при некотором выборе ДПСК.

Определение 2. Эллипс есть геометрическое место точек (плоскости), для каждой из которых сумма расстояний до двух данных точек (называемых

фокусами) есть величина постоянная (большая расстояния между фокусами).

III Элементы эллипса

Эллипс имеет две оси симметрии, которые называются осями эллипса. Точка пересечения осей – это центр эллипса. Точки пересечения эллипса со своими осями – это вершины эллипса. Отрезки осей между вершинами и их длины также называют осями: большая ось (на ней лежат фокусы) и малая ось. Половины этих осей называют полуосями (большая и малая). Кроме того, для любой точки M эллипса отрезки MF ₁ и MF ₂ и их длины r ₁ и r ₂ называют фокальными радиусами этой точки (формулы для фокальных радиусов см. пункт II).

Пример. Найти элементы эллипса .

Полуоси: – большая,

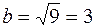– малая.

Вершины: A ₁(–5;0), A ₂(5;0), B ₁(0;–3), B ₂(0;3).

Расстояние между фокусами: .

Фокусы: F ₁(–4;0), F ₂(4;0).

IV Нормальное уравнение эллипса.

Исходя из определения 2, выберем ДПСК так, чтобы центр эллипса имел координаты (x ₀, y ₀), а его оси были параллельны координатным осям. В этой системе эллипс будет определяться уравнением

. (3)

К этому же уравнению приходим и исходя из определения 1 после параллельного переноса системы координат в точку (–x ₀; –y ₀).

Фокусы эллипса (3) лежат на прямой y=y ₀, если a>b, и на прямой x=x ₀, если a<b.

V Параметрические уравнения эллипса (1):

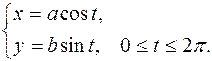
Замечание. Окружность – это частный случай эллипса, когда a=b.

А эллипс можно понимать как деформированную окружность.

Типовые задачи. 1). Составить каноническое уравнение эллипса, зная некоторые из его элементов. 2). Общее уравнение эллипса, например x ² + 4 y ² + 4 x– 8 y– 8 = 0, привести к нормальному виду и найти элементы эллипса. 3). Выяснить, какую линию определяет уравнение .

ЛЕКЦИЯ 10

I Каноническое уравнение гиперболы

Определение 1. Гиперболой называется линия, которая в некоторой ДПСК имеет уравнение

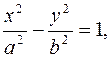(1)

где a и b – некоторые положительные числа.

Гипербола (как и эллипс) симметрична относительно обеих осей координат. В первой четверти уравнение (1) эквивалентно уравнению

. (2)

При 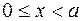гипербола (2) не существует, y (a) = 0 и при стремлении x в 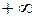, у также стремится в 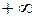. Чтобы выяснить характер этого стремления, рассмотрим прямую и найдем расстояние d (M, p), где M (x, y)– текущая точка гиперболы (2):

Умножая и деля полученное выражение на , получим

.

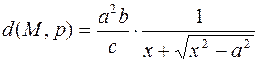Теперь нетрудно заметить, что 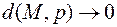при 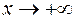, т.е. гипербола (2) приближается к прямой p. Эту прямую (а с ней и прямую 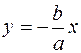в

силу симметрии) называют асимптотой гиперболы.

II Определяющее свойство гиперболы

Обозначим 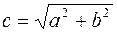и рассмотрим точки F ₁(–c;0) и F ₂(c;0) (их называют фокусами гиперболы). Можно доказать (докажите!), что для любой точки M гиперболы (1) имеет место соотношение

.

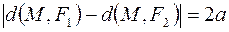Как и для эллипса, это свойство можно взять за определение и получить каноническое уравнение (1) в некоторой ДПСК.

Определение 2. Гипербола есть геометрическое место точек (плоскости), для каждой из которых модуль разности расстояний до двух данных точек (называемых фокусами гиперболы) есть величина постоянная

(меньшая расстояния между фокусами).

III Элементы гиперболы

Оси симметрии гиперболы называют, обычно, просто ее осями, а точку их пересечения – центром гиперболы. Для канонической гиперболы – это оси координат и начало координат. Точки пересечения гиперболы со своими осями – это вершины гиперболы. Гипербола (1) имеет две действительные вершины A ₁(–a;0) и A ₂(a;0) и две “мнимые” вершины B ₁(0;– b) и B ₂(0; b). Отрезок A ₁ A ₂и его длина 2 а называется действительной осью гиперболы (1), а отрезок B ₁ B ₂ и его длина 2 b – мнимой осью (a и b – полуоси, действительная и мнимая). Прямоугольник со сторонами 2 a и 2 b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах называется основным прямоугольником гиперболы. Диагонали этого прямоугольника – прямые – это асимптоты гиперболы.

Для любой точки M гиперболы

отрезки MF ₁ и MF ₂ и их длины

r ₁ и r ₂ называются фокальными

радиусами этой точки.

Гипербола состоит из двух частей,

которые называются ветвями.

IV Нормальное уравнение гиперболы

Гипербола, центр которой имеет координаты (x ₀; y ₀), а оси парал- лельны координатным осям, имеет уравнение

. (3)

Фокусы этой гиперболы лежат на прямой y=y ₀.

Замечание 1. Уравнение вида

(4)

также определяет гиперболу. Ее фокусы и действительные вершины лежат на оси Oy. Гиперболы (1) и (4) в одной и той же системе координат и при одних и тех же значениях полуосей a и b называются сопряженными друг с другом.

Замечание 2. Гипербола с равными полуосями (a=b) называется равносторонней. Каноническое уравнение такой гиперболы пишут в виде

x ² –y ² =a ². Ее асимптоты взаимно перпендикулярны.

Типовые задачи аналогичны задачам для эллипса.

Дата добавления: 2015-06-28