Пример 2

Задается: схема нагружения балки (рис. 9), длины участков балки: b=2a, a, распределенная нагрузка интенсивностью q, величина сосредоточенной силы F=3qa, величина изгибающего момента M=qa².

Требуется: построить эпюры перерезывающей силы Q_y и изгибающего момента M_x при известной нагрузке и схеме нагружения балки.

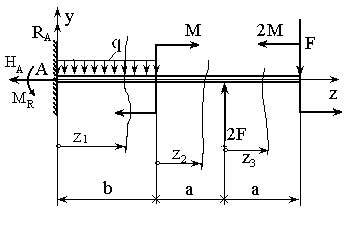
Рис. 9. Схема нагружения балки.

РЕШЕНИЕ

1. Определение опорных реакций (рис. 9).

Для определения опорных реакций составляются уравнения равновесия балки:

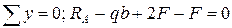, откуда .

.

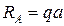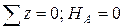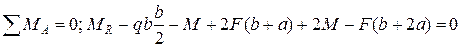, откуда .

Впоследствии нет необходимости составлять уравнение равновесия 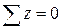, так как при указанной схеме нагружения составляющая 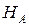всегда равна нулю.

2. Разбивка балки на участки.

Для построения эпюры перерезывающей силы 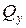и изгибающего момента 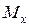необходимо рассмотреть три участка с координатами 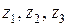(рис. 11).

3. Определение законов изменения перерезывающей силы 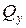и изгибающего момента 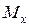по участкам балки.

Начало рассматриваемых участков необходимо обозначать точкой, текущее значение 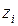стрелкой. Начало последующего участка начинается на границе предыдущего участка.

3.1. Первый участок.

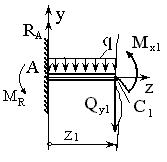
Рис. 10. К определению и 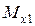на первом участке.

Координата 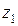для первого участка изменяется в пределах 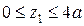. Уравнения равновесия для отсеченной (левой) части балки имеют вид:

.

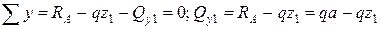Перерезывающая сила на границах участка принимает значения:

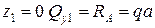при , при .

.

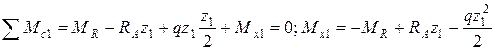Изгибающий момент на границах участка принимает значения:

при ,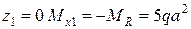

при .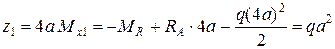

В координатах M_x1-z₁ полученное выражение изгибающего момента M_x1 описывает кривую второго порядка. Определим выпуклость кривой:

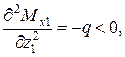следовательно кривая выпукла вверх.

Условие экстремума кривой: 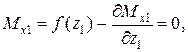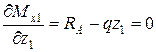, следовательно, функция имеет экстремум при .

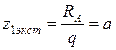Вычислим величину изгибающего момента при :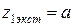

.

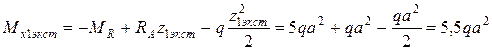3.2. Второй участок (рис. 11).

Рис. 11. К определению и 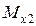на втором участке.

На втором участке координата 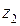изменяется в пределах .

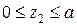Уравнения для отсеченной (левой) части балки имеют вид:

.

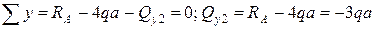На втором участке перерезывающая сила постоянна по длине участка .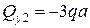

;

.

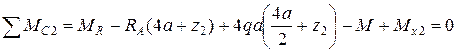Изгибающий момент на границах участка принимает значения:

при ,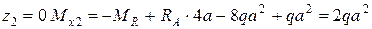

при .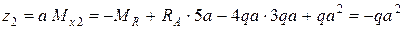

3.3. Третий участок (рис. 12).

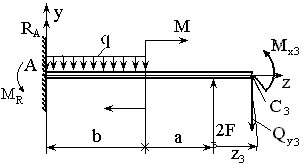
Рис. 12. К определению 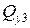и 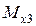на третьем участке.

На третьем участке координата 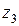изменяется в пределах .

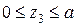Уравнения равновесия для отсеченной (левой) части балки имеют вид:

.

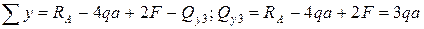На третьем участке перерезывающая сила постоянна по длине участка .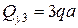

;

.

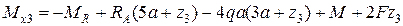Изгибающий момент на границах участка принимает значения:

при ,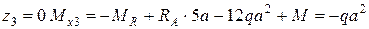

при .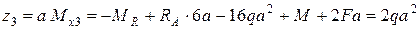

По результатам вычислений строятся эпюры перерезывающей силы 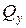и изгибающего момента 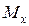(рис. 13).

4. Выполняем проверку правильности построения эпюр 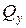и .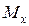

4.1. На участке АВ, где действует распределенная нагрузка q:

- эпюра 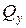- наклонная прямая;

- эпюра 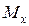- кривая второго порядка;

- в сечении 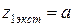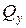=0, а изгибающий момент принимает экстремальное значение .

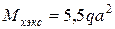4.2. В сечениях К, А, С и В, где приложены сосредоточенные силы на эпюре 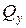имеют место «скачки» на величину приложенных сил.

4.3. В сечении В и К, где приложен сосредоточенный момент на эпюре 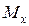имеет место «скачок» на величину данного момента.

4.4. На участках балки, где 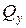положительна эпюра 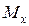возрастает.

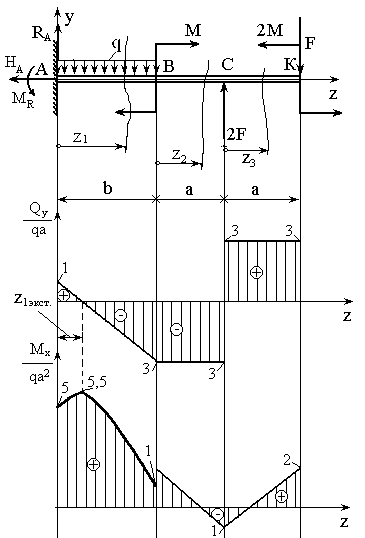
Рис. 13. Расчетная схема бруса, эпюры перерезывающей силы 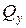и изгибающего момента .

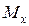Дата добавления: 2015-06-29