Расчет на прочность

4. Из условия прочности по нормальным напряжениям определяем ве­личину необходимого осевого момента сопротивления сечения балки. Условие прочности по нормальным напряжениям имеет вид:

Для стали 45 предел текучести 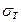=600МПа, примем коэффициент запаса прочности п_Т = 2. И вычисляем допускаемое напряжение

Так как в опасном сечении , следовательно из условия прочности определяем необходимый осевой момент сопротивления сечения балки:

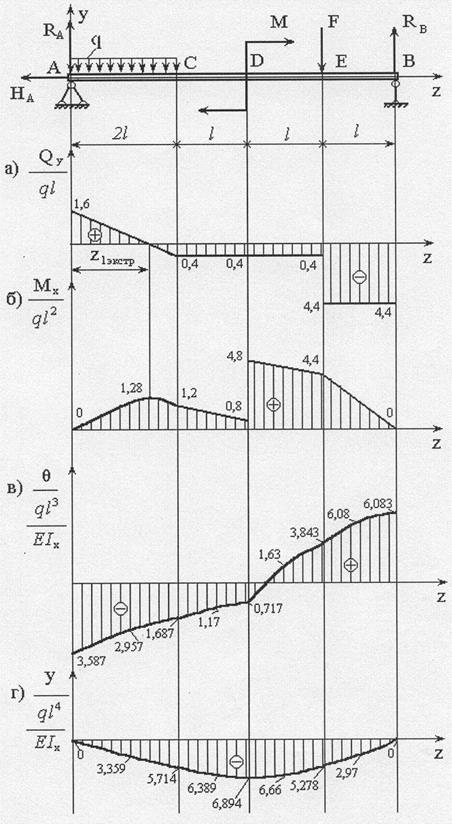
Рис. 24. Расчетная схема бруса, эпюры перерезывающей силы Q_y, изгибающего момента М_х, углов поворота θ и прошибов у.

5. Подбираем сечения по величине необходимого осевого момента со­противления изгибу.

5.1. Прямоугольное сечение балки:

Примем h = 2b для прямоугольного сечения имеем.

принимая W_x = 200 см, определяем размер

Площадь сечения А₁=bh =6,7·2·6,7=89,78 см².

5.2. Квадратное сечение балки:

Для квадратного сечения имеем , откуда

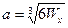. Поскольку W_x = 200 см³, то

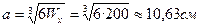. Площадь сечения

А₂ =10,63²=112,99 см².

5.3. Круглое сечение балки:

Для круглого сечения , следовательно

Поскольку W_x = 200 см³, то Площадь сечения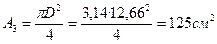

5.4. Кольцевое сечение балки:

Задается D = 1,25 d. Для кольцевого сечения 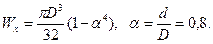Поскольку W_x =200 см³, то

Площадь сечения

5.5. Двутавровое сечение балки:

По таблице сортамента (ГОСТ 8239-72) ближайший осевой момент сопротивления W_xmабл = 203 см³. Это­му моменту сопротивления соответствует двутавр №20а с площадью поперечного сечения А₅=28,9см². Поскольку табличное значение осевого момента

W_xmaбл несколько отличается от расчетного значения W_x, то

6. Определение процента напряжения и перенапряжения материала
балки по отношению к допускаемому напряжению для двутаврового сече­
ния.

7. Оцениваем экономичность подобранных сечений по отношению к
наименьшему (двутавровому), принимая площадь А₅ за 100%.

A₅:A₄:A₃:A₂:A₁=100:460:432:390:310%

Следовательно, наиболее экономичным с точки зрения металлоемко­сти является двутавровое сечение балки.

8. Оценка прочности балки двутаврового сечения по касательным на­
пряжениям.

Условие прочности по касательным напряжениям имеет вид:

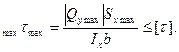
Из эпюры поперечных (перерезывающих) сил (рис.24) . Из таблицы сортамента (ГОСТ 8239-72) для двутавра №20а находим S_xmax =114см³, I_x = 2030см⁴, b=d = 0,52 см. По третьей теории прочности [τ]= 0,5[σ] = 0,5·300 = 150МПа.

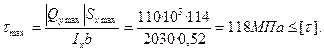
Следовательно, условие прочности по касательным напряжениям вы­полняется.

9. Выбор опасного сечения.

В рассматриваемом примере опасным является сечение D (рис. 24), где действует и .

10. Построение эпюры нормальных напряжений в опасном сечении.

Нормальные напряжения в опасном сечении (сеч. D) вычисляются по формуле.

где у_i- расстояние от оси х до рассматриваемого слоя.

Поскольку в опасном сечении М_хmax > 0, то слои, расположенные выше нейтральной линии, будут испытывать сжатие, ниже нейтральной линии – растяжение (рис. 25).

11. Построение эпюры касательных напряжений в опасном сечении.

Представим условно двутавровое сечение как фигуру, состоящую из трех прямоугольников: двух полок размером b·t и стенки размером (h - 2 t)·d, выбираемыми из таблицы сортамента. Касательные напряже­ния в точках D, E, F, G, К, L, М определяются по формуле Д. И. Журавско-го (Рис. 25. б):

12.1. Точка D.

следовательно

12.2.Точка Е.

I_x = 2030 см⁴; b = 11 см; h = 20 см; t = 0,86 см.

12.3. Точка F.

I_x =2030 см⁴; =90,53 см³; d = 0,52 см. Поскольку в точке F шири­на рассматриваемого слоя b = d = 0,52 см, следовательно касательное на­пряжение равно:

12.4. Точка G.

I_x =2030 см⁴; 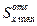=114 см³; b=d = 0,52 см.

12.5.-12.7. Точки K,L,M.

Поскольку эпюра касательных напряжений т симметрична относи­тельно оси х, то расчет в точках К, L, М можно не выполнять.

13. Проверяем прочность балки двутаврового сечения по эквивалент­
ным напряжениям.

Наиболее опасным с точки зрения прочности по эквивалентным на­пряжениям являются точки F и К. Условие прочности для точки F по третьей теории прочности запишется:

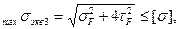
откуда

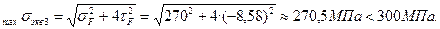
Таким образом, условие прочности по эквивалентным напряжениям для балки двутаврового сечения №20а выполняется.

14. Проверяем прочность балки двутаврового сечения по эквивалент­
ным напряжениям в сечении Е (рис. 24), так как в этом сечении изгибающий момент М_х близок к максимальному значению М_х =4,4 ql ², а попе­речная сила Q_y значительно больше, чем в опасном сечении D - Q_ymax =-4,4 ql. Проверка осуществляется для слоя F сечения балки.

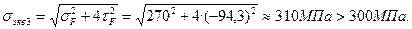
Условие прочности не выполняется, следовательно для дальнейших расчетов принимаем двутавр №22 с параметрами: I_x = 2550 см⁴, W_х =232см³, S_x =131см³, h =220мм, b =110мм, t =8,7мм, d =5,4 мм.

Вновь вычисляем напряжения в слое F:

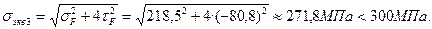
Условие прочности выполняется, следовательно для расчетов на прочность принимается двутавр №22.

Рис. 25. Эпюры нормальных (а) и касательных (б) напряжений в

опас­ном сечении балки.

15. Расчет балки двутаврового сечения на жесткость.

Для выполнения расчетов необходимо составить расчетную схему (рис. 26). С этой целью начало координат располагают в крайнем левом сечении балки, прерывающуюся распределенную нагрузку q продлеваем до крайнего правого сечения, и добавляем аналогичную нагрузку интен­сивностью q, но направленную в противоположную сторону.

Универсальное уравнение для углов поворота заданной балки имеет вид:

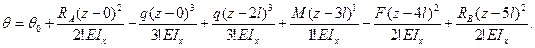
Универсальное уравнение прогибов заданной балки имеет вид:

Приведенные варианты справедливы соответственно в пределах пер­вого, второго, третьего и четвертого участков балки. Постоянные у₀ и θ₀ представляют собой прогиб и угол поворота крайнего левого сечения бал­ки (сеч. А) и называются начальными параметрами. Их определяют из гра­ничных условий – условий закрепления балки. Поскольку балка опирается на опоры в сечениях А и В, следовательно линейные перемещения в этих сечениях отсутствуют, то есть:

а) если z= 0, то у =0

б) если z= 5 l, то y= 0

Рис. 26. Схема к составлению универсальных уравнений прогибов и

углов поворота сечений балки.

Используя граничное условие (а) для уравнения прогибов на первом участке, имеем:

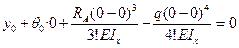, следовательно y₀ =0.

Используя граничное условие (б) для уравнения прогибов на четвер­том участке, имеем:

следовательно

Вычисляем значения y_i и θ_i по границам и в середине участков.

1.

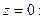
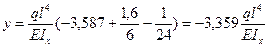
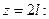
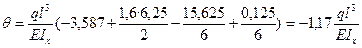
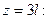
Расчеты углов поворота θ и прогибов у для точек z =3,5 l; z =4 l; z =4,5 l; z =5 l выполняются аналогично.

Полученные значения сводим в таблицу.

Координата сечения	Угловое перемещение сечения;	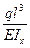Линейное перемещение сечения;
0	-3,587
1	-2,957	-3,359
21	-1,687	-5,714
2,51	-1,17	-6,3899
31	-0,717	-6,894
3,51	1,63	-6,66
41	3,843	-5,278
4,51	6,08	-2,97
51	6,083

По полученным значениям строим эпюры углов поворота и прогибов (рис.24.в,г).

Выполняется проверка жесткости балки по условию жесткости.

Поскольку [ у ] = 1 см, то y_max =0,422 < [ у ] = 1 см, следовательно балка двутаврового сечения №22 удовлетворяет условию жесткости. В случае, если условие жесткости не выполняется, то подбор сечения выполняется из условия жесткости, из которого следует, что для данной балки осевой момент инерции равен:

По полученному значению I_x выбирается из сортамента необходимый

профиль. При расчетах на жесткость обычно принимаются значения до пускаемого прогиба [ у ] = (0,001..,0,002) L, где L - длина балки.

ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ

1. Что называется балкой? Привести три типа опорных закреплений и по­казать на них опорные реакции.

2. Дать определение прямого поперечного изгиба и прямого чистого изги­ба.

3. Построить эпюры поперечных сил и изгибающих моментов для задан­ной балки. Объяснить правило знаков для поперечных сил и изгибаю­щих моментов.

4. Привести дифференциальные зависимости между поперечной силой, изгибающим моментом и внешними нагрузками.

5. Написать формулу для определения нормального напряжения при изги­бе. Построить эпюру распределения нормального напряжения по высо­те прямоугольного и двутаврового сечений балки.

6. Что называется осевым моментом сопротивления?

7. Дайте определение опасного сечения балки, опасного слоя.

8. Запишите условие прочности балки по нормальным напряжениям.

9. Привести наиболее выгодные формы сечений балок при изгибе (по рас­ходу материала).

10. Поясните причину появления касательных напряжений при поперечном

11. изгибе балок.

12. Запишите условие прочности балки по касательным напряжениям.

13. Приведите формулу Д. И. Журавского.

14. Постройте эпюру распределения касательных напряжений по высоте прямоугольного и двутаврового сечений.

15. Запишите условие прочности по эквивалентным напряжениям.

16. Изложите методику определения перемещений при изгибе с помощью приближенного дифференциального уравнения изогнутой оси балки.

17. Запишите универсальные уравнения для углов поворота и прогибов балки.

18. Какие условия необходимо соблюдать для правомерного использования универсальных уравнений?

19. Как определяются начальные параметры в универсальных уравнениях?

20. Запишите условие жесткости балки. 20.Как назначается допускаемый прогиб балки?

21. Как продолжить расчет, если прочность балки обеспечена, а условие жесткости не выполняется?

Дата добавления: 2015-06-29