Механические свойства материалов

Рекомендуемая литература

1. Ковалев В.В. Практикум по финансовому менеджменту. Конспект лекций с задачами. М.: Финансы и статистика, 2000. – 288 с.

2. Ковалев В.В. Практикум по анализу и финансовому менеджменту. Конспект лекций с задачами и тестами. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2008. – 448 с.

3. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. – 2-е изд., перераб и доп. – М.: Финансы и статистика, 2002. – 544 с.

4. Красс М.С., Чупрынов Б.П. Математика для экономистов. – СПб.: Питер, 2010. – 464 с.

5. Мелкумов Я.С. Финансовые вычисления. Теория и практика: Учеб. – справ. пособие. – М.: ИНФРА – М, 2007. – 408 с.

6. Родзиковская Т.А. Финансово-экономические расчеты: Методические рекомендации. – Иркутск: Изд-во ИрГТУ, 2005. – 24 с.

7. Салин В.Н., Ситникова О.Ю. Техника финансово – экономических расчетов: Учеб. пособие. – М.: Финансы и статистика, 200. – 80 с.

8. Статистика финансов: учеб. для студентов, обучающихся по специальности «Статистика»/под ред. М.Г. Назарова. – М.: Изд-во Омега-Л, 2005. – 460 с.

9. Финансовый словарь / Благодатин А.А., Лозовский Л.Ш., Райзберг Б.А. – М.: ИНФРА-М, 2008. – 378 с.

10. Четыркин Е.М., Васильева Н.Е. Финансово – экономические расчеты: справочное пособие. – М.: Финансы и статистика, 1990. – 302 с.

11. Четыркин Е.М. Финансовая математика: Учебник. – 7-е изд., испр. – М.: Дело, 2007. – 400 с.

12. Шарп У., Александер Г., БейлиДж. Инвестиции. – М.: ИНФРА-М, 2004. – 1028 с.

13. Ширшов Е.В. Финансовая математика: учебн. пособие / Е.В. Ширшов, Н.И. Петрик, А.Г. Тутыгин, Г.В. Серова. – 4-е изд., стер. – М.: КНОРУС, 2007. – 144 с.

14. Яковлева А.В. Статистика финансов. Ответы на экзаменационные вопросы: учебное пособие для вузов.: Изд-во «Экзамен», 2006. – 126 с.

ПРИЛОЖЕНИЯ

Образец титульного листа

Министерство сельского хозяйства Российской Федерации

Федеральное агентство по сельскому хозяйству

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Иркутская государственная сельскохозяйственная академия

Кафедра информатики и математического моделирования

Контрольная работа

«Основы финансовых вычислений»

Выполнил:

Студент 2-го курса,

экономического факультета

направления 080100.62 – «Экономика»

Ф.И.О.

№ зачетной книжки

Проверил:

доцент кафедры информатики и математического моделирования

Барсукова М.Н.

Иркутск 2013

Механические характеристики определяются путем испытания стандартных образцов. Для каждого материала устанавливаются государственным стандартом форма и соотношение размеров образцов для определения в лабораторных условиях их механических свойств. Образцы испытываются в зависимости от материала на растяжение, сжатие, изгиб, кручение, срез. Основным видом испытаний стали является растяжение стандартных круглых или плоских образцов, для которых строятся диаграммы растяжения в координатах сила – абсолютное удлинение 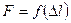. Для определения обобщенных механических характеристик материала диаграммы строят в координатах напряжение – деформация , которые определяются по формулам .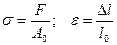

На отрезке от точки А до точки В линейная зависимость нарушается, но при разгрузке образца возникшие деформации исчезают. Напряжение , соответствующее точке В, называется пределом упругости. Для стали предел упругости практически совпадает с пределом пропорциональности.

Практически горизонтальный отрезок CD называется площадкой текучести, а соответствующее напряжение - пределом текучести.

Пари напряжениях, равных пределу текучести, в малоуглеродистых сталях развиваются пластические деформации, связанные с необратимыми деформациями сдвига между кристаллами феррита. На хорошо отшлифованной поверхности образцов можно видеть наклоненные под углом 45⁰ к оси стержня полосы, называемые линиями Людерса-Чернова по имени немецкого и русского металлургов, впервые независимо друг от друга описавших это явление. Эти линии вызваны деформациями сдвига от наибольших касательных напряжений, действующих под углом 45⁰ к направлению действия силы F.

После развития определенных пластических деформаций и перестройки кристаллической решетки стали несущая способность стержня увеличивается - рост деформаций сопровождается увеличением напряжений, происходит упрочнение стали. Участок DE на диаграмме называется зоной упрочнения.

При напряжениях, соответствующих наивысшей точке Е на диаграмме, в определенном участке образца появляется значительное уменьшение размеров поперечного сечения – образуется, так называемая, шейка. Напряжение , соответствующее точке Е диаграммы, называется пределом прочности или временным сопротивлением.

Разрушение образца наступает вскоре после образования шейки. Истинное напряжение при разрыве определяется отношением .

Рассмотренная диаграмма называется условной, так как при ее построении не учитывается уменьшение площади поперечного сечения при растяжении образца. Диаграмма растяжения, построенная с учетом изменения площади поперечного сечения, называется истинной диаграммой. До предела текучести истинная и условная диаграммы практически совпадают. Заметное их отличие проявляется при напряжениях выше предела текучести, нарастая к концу стадии упрочнения. В силу того, что для пластичных материалов за опасное (предельное) напряжение принимается предел текучести, истинная диаграмма, как правило, не имеет практического значения.

Если довести нагружение образца до точки, лежащей выше предела упругости (точка М), а затем снять нагрузку, то диаграмма разгрузки пойдет по прямой ММ₁, параллельной ОА, а отрезок ОМ₁ будет соответствовать остаточной деформации . Отрезок М₁М₂ характеризует упругую деформацию 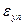при нагружении образца до точки М.

При повторном нагружении образца от точки М₁ диаграмма нагружения следует по кривой, практически совпадающей с прямой ММ₁. Таким образом, при повторном нагружении как бы повышается предел пропорциональности стали, что с вязано с изменением микроструктуры в кристаллической решетке. При этом площадка текучести исчезает, материал становится более хрупким. Изменения свойств стали, возникающие при разгрузке и повторном нагружении, называются наклепом. Это явление используется в технике, например, при изготовлении цепей грузоподъемных машин. Участок диаграммы ММ₁М называется петлей гистерезиса.

Получаемые по диаграмме растяжения пределы текучести и прочности , называются характеристиками прочности.

По результатам испытаний образца после разрыва определяются относительное остаточное удлинение 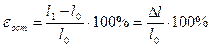и относительное остаточное сужение в шейке . Величины и характеризуют пластические свойства стали. Для стали марки ВСт3 они составляют .

Многие материалы имеют диаграмму растяжения, существенно отличающуюся от диаграммы растяжения для стали ВСт3. Например,

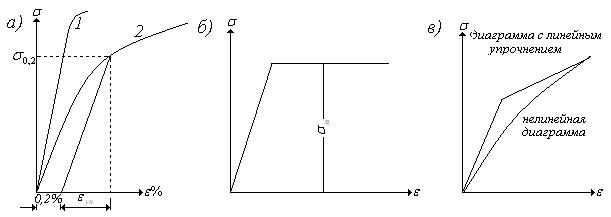
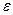На рис. а) показаны диаграммы для чугуна (1) и меди (2). Диаграмма (1) характерна тем, что практически до разрушения зависимость между и является линейной. Такие материалы называются хрупкими. К хрупким материалам относятся чугун, стекло, камень, инструментальные стали.

Диаграмма (2) с самого начала имеет нелинейный характер и соответствует пластичным материалам, у которых отсутствует площадка текучести. Для таких материалов принимается условный предел текучести, соответствующий напряжению, при котором остаточные деформации составляют 0,2%. В соответствии с этим условный предел текучести обозначается . Необходимо отметить, что в материале, наряду с пластическими, возникают и упругие деформации исчезающие после разгрузки.

Использование реальных диаграмм в расчетах часто приводит к большим математическим трудностям. Существуют различные способы аппроксимации этих диаграмм с помощью более простых графиков. Так например, для стали ВСт3, у которой пределы пропорциональности, упругости и текучести, имеют близкие значения, принимается диаграмма в виде двух прямых (рис. б), считая, что все три указанных напряжения соответствуют одной точке. Такая диаграмма называется диаграммой Прандтля. Она отражает одну из характерных особенностей поведения упруго-пластических материалов – способность к большим пластическим деформациям. В силу своей простоты эта диаграмма широко используется в расчетах конструкций, напряжения в которых превышают предел упругости. Диаграмма Прандтля, тем не менее, не полностью отражает реальное поведение материалов, и в расчетах могут использоваться более сложные диаграммы (рис. в).

Для испытания стали на сжатие применяют цилиндрические образцы высотой равной от одного до трех диаметров. Диаграмма сжатия пластической малоуглеродистой стали в интервале до предела текучести такая же, как и при растяжении. Пределы пропорциональности, упругости и текучести, а также модуль упругости у сталей при растяжении и сжатии практически одинаков. Предел прочности при сжатии у пластичной стали получить невозможно (образец вначале принимает бочкообразную форму, а затем, не разрушаясь, превращается в диск). Площадка текучести при сжатии стали не выражена, а зависимость между напряжениями и деформациями за пределом упругости имеет другой характер, чем при растяжении.

Хрупкие материалы имеют значительно меньший предел прочности при растяжении, чем при сжатии. Например, серый чугун при сжатии имеет предел прочности 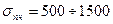МПа, а при растяжении МПа. Разрушение чугуна при сжатии начинается с образования трещин под углом 45⁰ к оси цилиндрического образца. Характер разрушения хрупких материалов при сжатии во многом зависит от сил трения, возникающих по контакту опорной плиты пресса с торцевой поверхностью образца.

Существенное влияние на механические свойства материалов могут оказывать такие факторы, как изменение температуры, технологические условия обработки при высоких температурах, радиоактивное облучение, скорость нагружения. Рассмотренные свойства стали соответствуют температуре 20⁰. В реальных условиях строительные конструкции могут эксплуатироваться при воздействии как высоких, так и низких температур. Для большинства металлов с повышением температуры уменьшаются пределы пропорциональности, текучести, прочности и модуль упругости, а характеристики пластичности (остаточная деформация и и остаточное сужение поперечного сечения увеличиваются). В области отрицательных температур повышается хрупкость металлов и увеличиваются значения . При этом пластические свойства понижаются.

При эксплуатации атомных электростанций, синхрофазотронов и других сооружений конструкции находятся под воздействием ионизирующего облучения, которое приводит к изменению механических свойств материалов. Действие радиационного облучения на металлы аналогично понижению температуры, то есть повышает прочностные характеристики и понижает пластические свойства. При длительной работе бетонных сооружений под воздействием радиации происходит понижение их жесткостных свойств и уменьшение модуля упругости.

На проявление упругих и пластических свойств материалов влияет скорость приложения нагрузки. Например, для стали при быстром нагружении пластические свойства не успевают развиться и на диаграмме растяжения отсутствует площадка текучести,, а предел прочности увеличивается.

Существенное значение для некоторых материалов имеет длительность действия нагрузки, так как в этом случае проявляется свойство ползучести, которое характеризуется нарастанием деформаций при постоянной нагрузке.

У металлов свойства ползучести проявляются только при повышенных температурах (>400⁰). График изменения деформаций во времени стального образца при высокой температуре представлен на рис. а). Участок ОА соответствует упругим «мгновенным» деформациям, возникающим в момент приложения нагрузки (период нагружения считается малым по сравнению с рассматриваемыми длительными процессами).

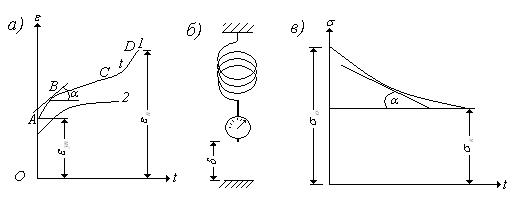
Далее при постоянной нагрузке развиваются деформации ползучести, с начала по кривой АВ, затем по прямой ВС и заканчиваются перед разрушением кривой CD. В теории ползучести вводится понятие скорости ползучести, определяемое по формуле 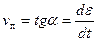(рис. а).

Участок АВ соответствует неустановившейся ползучести., ВС – установившейся ползучести 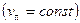и CD – прогрессирующей ползучести. Свойства ползучести учитываются в расчетах конструкций на прочность. Необходимо, чтобы наибольшая деформация ползучести в период эксплуатации не превышала допускаемой. Примером конструкций, работающих при высоких температурах и напряжениях, являются металлические паропроводы, у которых диаметр со временем увеличивается и может произойти разрыв стенок.

Бетон также обладает свойством ползучести. Ползучесть бетона проявляется при нормальной температуре. Со временем деформации ползучести затухают (кривая 2 на рис. б). Период затухания деформаций ползучести бетона длительный и может занимать несколько лет.

Рассмотрим релаксацию напряжений, которая характеризуется уменьшением напряжений при постоянной деформации. Она наблюдается в болтовых соединениях, когда усилие затяжки (плотность соединения) со временем уменьшаются. Релаксация напряжений (усилий) показана на схеме. б), где между двумя неподвижными плоскостями помещена пружина с динамометром, показывающим усилие растяжения. Если материал пружины обладает свойством релаксации, то показания динамометра со временем уменьшаются. График зависимости напряжений от времени – кривой релаксации показан на рис. в). Начальное напряжение 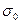создается в короткий промежуток времени при некотором фиксированном перемещении крюка динамометра до опоры. Затем напряжение (усилие) уменьшается сначала быстро, а затем с затуханием, приближаясь асимптотически к горизонтали на уровне конечного напряжения . Тангенс угла наклона касательной к кривой релаксации в некоторой точке дает по абсолютной величине численное значение скорости релаксации .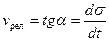

Явления ползучести и релаксации особенно заметно проявляются в различных полимерах, используемых в качестве конструкционных материалов при изготовлении элементов строительных конструкций.

Дата добавления: 2015-06-29