Конические сечения

Коническими сечениями называются линии, которые получаются при пересечении поверхности конуса второго порядка с плоскостью. К числу этих линий относятся следующие: окружность, двойная прямая, две пересекающиеся прямые, эллипс, парабола, гипербола. Простейшим коническим сечением является точка.

Рассмотрим все виды конических сечений и условия, при которых они получаются, на примере конуса вращения, пересеченного проецирующими плоскостями рис. 141:

1) точка S, когда плоскость a пересекает только вершину конуса (рис. 141а);

2) окружность, когда секущая плоскость перпендикулярна к оси конуса (рис. 141б);

3) двойная прямая, когда секущая плоскость является предельной, т. е. касательной к поверхности конуса (рис. 141в);

4) две пересекающиеся прямые, когда секущая плоскость проходит через вершину (рис.);

5) эллипс, когда плоскость пересекает все образующие конуса

и когда она не перпендикулярна его оси (рис. 141а).

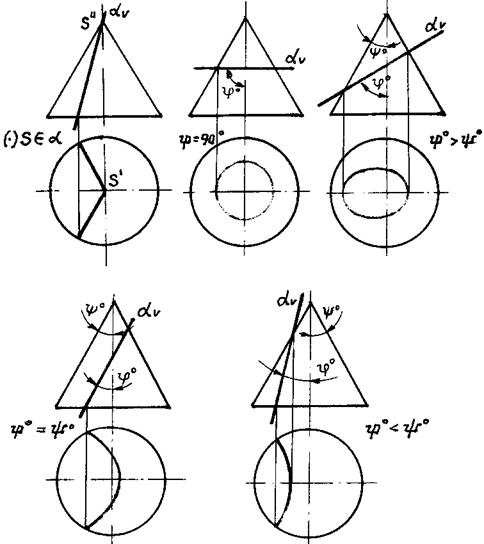
Рис. 141

Признак, при котором получится эллипс, может быть выражен еще иначе. Обозначим половину угла при вершине конуса через j, а угол наклона секущей плоскости к оси конуса — через y. Тогда

y^o > j^o.

Для построения фронтальной проекции эллипса вначале отмечаем опорные точки А и В. Отрезок А”В” — фронтальная проекция большой оси эллипса (всей фигуры сечения).

Горизонтальная проекция эллипса строится по фронтальной. Для этого отрезок А”В” делится точкой С” пополам. В точку С”º D ” спроецируется малая ось эллипса, перпендикулярная к плоскости проекций V.

Для построения горизонтальных проекций промежуточных точек проводим ряд вспомогательных горизонтальных плоскостей (b₁,b₂,b₃), каждая из которых пересекает поверхность конуса по окружности соответствующего радиуса, а плоскость a — по горизонтали, перпендикулярной плоскости V.

На пересечении горизонтальных проекций окружностей с горизонтальными проекциями горизонталей находятся горизонтальные проекции искомых точек.

Натуральная величина эллипса может быть легко построена методом замены плоскостей проекций. Для этого на произвольном расстоянии проведена ось симметрии фигуры сечения (большая ось эллипса), параллельно фронтальному следу проецирующей плоскости a, и в обе стороны от нее перпендикулярно отложены величины, взятые с горизонтальной проекции фигуры сечения (так как горизонтальные проекции хорд эллипса, параллельные его малой оси, равны их натуральной величине) (рис. 142).

Рис. 142

6) Парабола, когда секущая плоскость параллельна одной из образующих конуса; в этом случае y угол между плоскостью и осью конуса равен углу j между образующей и осью конуса (рис. 143). Фронтальная проекция параболы сливается со следом a₁ секущей плоскости. Для построения горизонтальной проекции параболы проводим ряд вспомогательных горизонтальных плоскостей (b₁,b₂), каждая из которых пересекает поверхность конуса по окружности, а плоскость a -- по горизонтали, перпендикулярной к плоскости V. В пересечении горизонтальных проекций этих горизонталей с горизонтальными проекциями соответствующих окружностей получаем точки D ', E', J ', K '. Горизонтальную проекцию A ' вершины параболы, а также горизонтальные проекции B ' и C ' точек, принадлежащих одновременно и окружности основания конуса получаем непосредственно, проводя линии из точек A '' и B ''º C '' (рис. 143).

Натуральная величина параболы строится аналогично натуральной величине эллипса (рис. 143).

Рис. 143

7) Гипербола, когда секущая плоскость параллельна оси конуса (рис. 144). В этом случае угол j равен нулю.

Так как секущая плоскость a - профильная плоскость, фронтальная и горизонтальная плоскости гиперболы являются отрезками прямых. Точки A '' и P'' являются фронтальными проекциями вершин параболы. Их горизонтальные проекции A 'º P' определяются по линии связи (рис. 144). Промежуточные точки D, E, J, K найдены с помощью вспомогательных горизонтальных плоскостей (b₁,b₂).

Для построения натуральной величины гипербола совмещена с плоскостью H путем вращения вокруг хорды BC. Если образующие конуса, которым параллельна плоскость a, ортогонально спроецировать на эту плоскость, то получим асимптоты гиперболы, которые совмещены с горизонтальной плоскостью проекций H (рис. 144).

Рис. 144

Дата добавления: 2015-06-29