Поверхности винтовые

Поверхности, образованные вращением окружности

В зависимости от взаимного расположения окружности и оси вращения можно получить различные поверхности (рис. 132).

Рис. 132

Тор (рис. 132а). Образуется вращением окружности а вокруг оси i, принадлежащей плоскости этой окружности а, но не проходящей через ее центр О. Это поверхность четвертого порядка.

Сфера (рис. 132б) — частный случай тора, когда центр О принадлежит оси вращения. Поверхность второго порядка.

Рис. 133

Глобоид (рис. 132в). Образующая — дуга окружности, обращенная выпуклостью к оси.

Ортогональные проекции тора, сферы, глобоида и построение проекций точки, принадлежащей названным поверхностям, показаны на рисунках 133, 134 и 135.

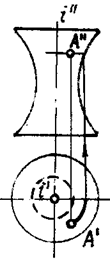Рис. 134 Рис. 135  

Винтовая поверхность получается винтовым перемещением образующей. Как известно, винтовое перемещение характеризуется вращением вокруг оси и одновременно поступательным движением, параллельным этой оси.

В зависимости от формы образующей, винтовые поверхности бывают линейчатые и нелинейчатые.

Винтовые поверхности широко применяются в машиностроении (резьба крепежных изделий, ходовых винтов, шнеков и др.).

Определитель винтовой поверхности:

F(a, m)[ A ],

где a — образующая (кривая или прямая);

m — направляющая — винтовая линия;

[ A ] — указания о характере винтового перемещения образующей.

Линейчатые винтовые поверхности называют ГЕЛИКОИДАМИ.

Если образующая пересекает ось, геликоид называют закрытым.

Если она скрещивается с осью, геликоид — открытый.

В зависимости от угла наклона образующей к оси, геликоиды различают

— прямые, когда угол равен 90^о;

— косые, когда угол произвольный, отличный от 0^о и 90^о.

На рис. 136 показан закрытый прямой геликоид. Закрытый косой геликоид изображен на рис. 137.

Закрытый прямой геликоид иногда называют винтовым коноидом.

Почему? Для ответа следует сравнить рис. 137 и рис. 122.

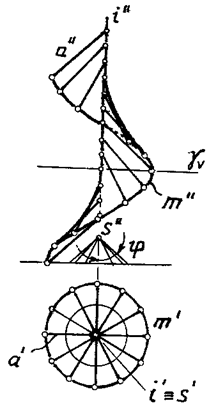  Рис. 136 Рис. 137

Дата добавления: 2015-06-29