Поверхности линейчатые

Линейчатые поверхности — поверхности, образующей которых является прямая. Они могут быть развертывающиеся и неразвертывающиеся.

Развертывающиеся поверхности — поверхности, которые после разреза их, например, по образующей, можно односторонне совместить с плоскостью без появления разрывов и складок (рис. 113).

Рис. 113

Неразвертывающиеся поверхности — поверхности, которые нельзя совместить таким образом с плоскостью.

У развертывающихся поверхностей смежные образующие параллельны или пересекаются.

У неразвертывающихся поверхностей смежные образующие скрещиваются.

Поверхности линейчатые развертывающиеся

Эти поверхности делятся на три вида:

— с одной направляющей и вершиной в собственной точке;

— с одной направляющей и вершиной в несобственной точке;

— с ребром возврата (торсы).

К поверхностям с одной направляющей и вершиной в собственной точке относятся коническая (направляющая — кривая) (рис. 114) и пирамидальная (направляющая — ломаная) (рис. 115).

Определитель имеет вид:

F(m)[(Sa Îm);(a ' S)],

причем “m” может быть соответственно или .

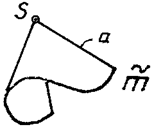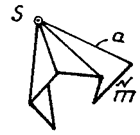Рис. 114 Рис. 115

К поверхностям с одной направляющей и вершиной в несобственной точке относятся цилиндрическая (направляющая — кривая) (рис. 116) и призматическая (направляющая — ломаная) (рис. 117).

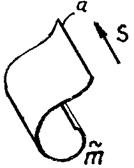Рис. 116 Рис. 117

Определитель имеет вид:

F(m)[(S_¥; (a || S)],

причем “m” может быть соответственно или .

Поверхность с ребром возврата имеет одну направляющую — пространственную кривую (ребро возврата). Образующая во всех своих положениях касательна к ребру возврата (рис. 118).

Рис. 118

Определитель имеет вид:

F(m)[ a U m]

Поверхности линейчатые неразвертывающиеся

Наиболее распространены в этой разновидности поверхностей поверхности Каталана или поверхности с двумя направляющими и плоскостью параллелизма. Образующие параллельны этой плоскости. Обычно принимают, что плоскости параллелизма совпадают с одной из плоскостей проекций, т.е. a || H или a || V.

В числе поверхностей Каталана различают: цилиндроид, коноид и косую плоскость или гиперболический параболоид.

Цилиндроид образуется, когда обе направляющие — кривые. Его определитель имеет вид:

F(, )[ a || a]

Цилиндроид общего вида и пример применения этого вида поверхности для соединения двух трубопроводов одинакового диаметра, оси которых пересекаются под некоторым углом, показаны на рисунке 119 и рисунке 120.

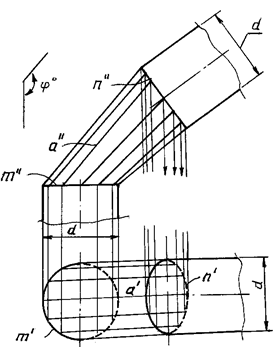Рис. 119 Рис. 120

Для случая (рис. 119) определитель имеет вид:

F(, )[ a || H]

Для случая (рис. 120) определитель имеет вид:

F(, )[ a || V]

Коноид образуется, когда одна направляющая — прямая, другая — кривая. Определитель имеет вид:

F(, 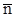)[ a || a]

На рисунках показаны коноид общего вида (рис. 121), коноид, у которого прямая направляющая перпендикулярна плоскости параллелизма (прямой коноид) (рис. 122) и аксонометрическая проекция, поясняющая происхождение названия “коноид”(рис. 123).

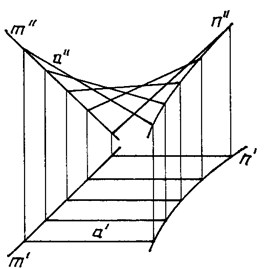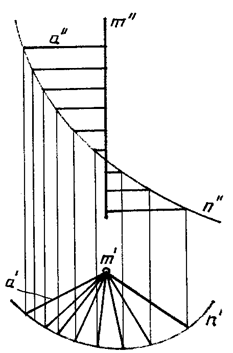Рис. 121 Рис. 122

Рис. 123

Косая плоскость или гиперболический параболоид образуется, когда обе направляющие — прямые (скрещивающиеся).

Для случая (рис. 124) определитель имеет вид:

F(, 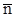)[ a || H]

Наглядное изображение косой плоскости показано на рис. 125.

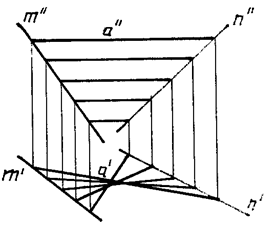Рис. 124 Рис. 125

Здесь a || H, то есть определитель имеет вид:

F(, )[ a || H]

Наглядное изображение косой плоскости при a || V показано на рис. 126

Рис. 126

Здесь m и n лежат в плоскостях, параллельных плоскости W. Определитель имеет вид:

F(, )[ a || V]

Дата добавления: 2015-06-29