Поверхности

ЛИНИЯ

ЛИНИИ И ПОВЕРХНОСТИ

План:

9.1. ЛИНИЯ

Винтовая линия

9.2. ПОВЕРХНОСТЬ

Поверхности линейчатые

Поверхности линейчатые развертывающиеся

Поверхности линейчатые неразвертывающиеся

Поверхности нелинейчатые

Поверхности параллельного переноса, вращения

Поверхности вращения

Поверхности винтовые

ЛИНИЯ — это множество всех последовательных положений движущейся точки.

Евклид: “Линия же — длина без ширины”.

Прямая — разновидность линии, которая получается, если движущаяся точка не изменяет направления движения.

Кривая — разновидность линии, которая получается, если движущаяся точка изменяет направление движения.

Плоские линии — линии, все точки которых принадлежат одной плоскости.

Пространственные линии (линии двоякой кривизны) — линии, все точки которых не принадлежат одной плоскости (например, линии пересечения поверхностей).

Алгебраические линии определяются алгебраическими уравнениями в декартовой системе координат (окружность, эллипс, парабола, гипербола и др.).

Трансцендентные линии описываются трансцендентными уравнениями (синусоида, спираль Архимеда и др.).

Если алгебраическое уравнение линии n ‑й степени, то алгебраическая кривая считается n ‑го порядка, то есть ПОРЯДКОМ КРИВОЙ называют наибольшую степень ее уравнения.

Геометрически порядок плоской кривой определяется наибольшим числом точек ее пересечения с прямой, лежащей в плоскости кривой, а для пространственной кривой — пересечением ее с плоскостью.

Для алгебраических кривых это число точек всегда конечно. Для трансцендентных — бесконечно. Например, для эллипса (рис. 108)

x ²/ a ² + y ²/ b ² = 1

имеем n = 2, т.е. это — кривая второго порядка.

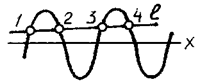Рис. 108 Рис. 109

Для синусоиды (рис. 109) y = sin x имеем n = ¥.

Кривые бывают закономерные и незакономерные, как, например, горизонтали на географической карте.

Винтовая линия

Пространственная кривая, широко применяемая в технике.

Цилиндрическая винтовая линия — пространственная кривая, получающаяся в результате двойного равномерного движения точки: вращения вокруг оси и поступательного движения вдоль прямой, параллельной этой оси (рис. 110).

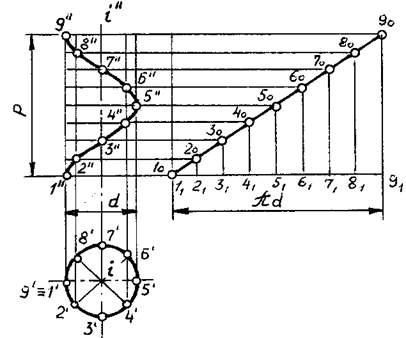
Рис. 110

p — шаг винтовой линии или расстояние между двумя ее соседними витками в направлении, параллельном оси i. Шаг определяет величину перемещения точки в направлении оси за один оборот этой точки вокруг оси.

Проекция цилиндрической винтовой линии на горизонтальную плоскость проекций (при i ^ H) — окружность, на фронтальную плоскость проекций — синусоида.

Отрезок [1_o1_o1] — развертка цилиндрической винтовой линии.

j^o — угол подъема винтовой линии.

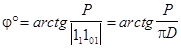
Цилиндрические винтовые линии бывают правые и левые. Основание для такого деления — направление движения точки, спускающейся по винтовой линии. Если проекция этого направления на плоскость, перпендикулярную к оси винтовой линии, совпадает с направлением движения часовой стрелки — винтовая линия ПРАВАЯ. В противном случае — ЛЕВАЯ.

Коническая винтовая линия — пространственная кривая, получающаяся в результате двойного равномерного движения точки: вращения вокруг оси и поступательного движения вдоль прямой, пересекающейся с этой осью (рис. 111).

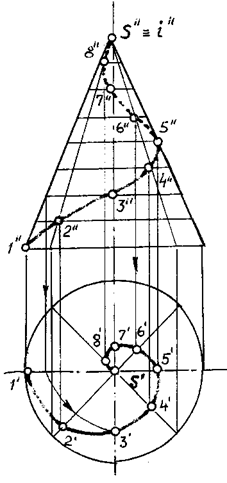
Рис. 111

При i ^ H горизонтальная проекция конической винтовой линии — архимедова спираль, фронтальная — затухающая синусоида.

С житейской точки зрения поверхность — внешняя сторона предметов. Так утверждают толковые словари. Евклид: “Поверхность есть то, что имеет только длину и ширину”.

В технической практике принято рассматривать образование поверхности (как и линии) с позиций кинематики — движения.

ПОВЕРХНОСТЬ — это множество последовательных положений движущейся линии — образующей.

Образующая может сохранять свою форму или изменять ее — деформироваться. Закон перемещения образующей определяется направляющими линиями, по которым скользит образующая и характером движения образующей. Например, поверхности Каталана (названы так по имени бельгийского ученого, их исследовавшего), или — поверхности с плоскостью параллелизма. Прямолинейная образующая “a” перемещается — скользит по двум направляющим — “n” и “m”, оставаясь параллельной плоскости параллелизма a.

Для изображения поверхности на чертеже, используют КАРКАС — множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае хотя бы одна линия каркаса. Проекции каркаса можно построить, если известен определитель поверхности.

ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ — совокупность независимых условий, однозначно задающих поверхность.

Различают две части определителя:

— геометрическая часть указывает на геометрические фигуры (точки, линии, поверхности), с помощью которых образовывается поверхность; обозначается (Г);

— алгоритмическая (описательная) часть содержит указания о характере изменения образующей и законе ее перемещения; обозначается [ A ].

Таким образом, определитель пишется в следующей форме:

F(Г)[ A ]

Определитель находят, исходя из кинематического способа образования поверхности. Например, для поверхностей Каталана:

F(m,n)[ a || a]

Для задания этих поверхностей на эпюре Монжа достаточно указать проекции направляющих m и n и положение плоскости параллелизма a (рис. 112).

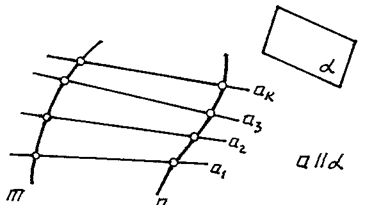
Рис. 112

В геометрическую часть определителя не записывают образующую a. Поверхность линейчатая (образующая — прямая линия). Поэтому априорно известно, что а — прямая.

В алгоритмической части содержится указание, что поверхность Каталана является поверхностью с плоскостью параллелизма. Поэтому в геометрическую часть определителя не записывают также и плоскость параллелизма.

Дата добавления: 2015-06-29