Дифференцирование единичного вектора

Вычисление производной от единичного вектора 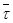по времени дает следующий результат .

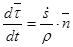Единичный вектор 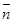перпендикулярен вектору 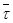, направленному по касательной к кривой и лежит в соприкасающейся плоскости. Вектор 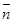направлен по главной нормали кривой в сторону ее вогнутости.

Ускорение точки при естественном способе задания движения.

Скорость точки равна .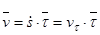

В соответствии с определением ускорения

.

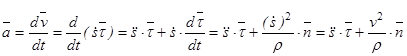Или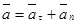

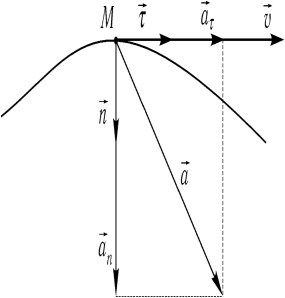
Таким образом получено разложение вектора ускорения точки по осям естественного трехгранника.

Часть ускорения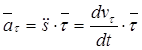

называется касательной составляющей ускорения.

Другая часть ускорения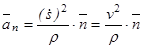

называется нормальной составляющей ускорения. Она направлена внутрь вогнутости траектории, т.е. в сторону положительного направления единичного вектора главной нормали .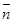

Формулы для проекции ускорения на естественные оси:

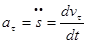
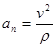
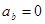
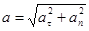
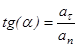
Касательная составляющая 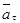, при 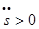направлена по направлению вектора 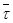, при 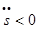противоположно .

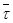Дата добавления: 2014-01-03