Отношения эквивалентности

Определение. Бинарное отношение 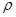на множестве А называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. Обычно отношение эквивалентности обозначается знаком ~ (или º). Для обозначения принадлежности упорядоченной пары (а, b) отношению ~ большей частью используют инфиксную запись, пишут 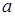~ b (читается: а эквивалентно ).

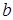Примеры отношения эквивалентности.

1. Отношение равномощности, заданное на произвольной системе конечных множеств. Эквивалентные множества имеют одинаковую мощность.

2. Отношение подобия, определенное на множестве всех треугольников евклидовой плоскости. Эквивалентные треугольники подобны.

3. Отношение параллельности, определенное на множестве всех прямых евклидовой плоскости. Эквивалентные прямые параллельны.

4. Отношение сравнимости по модулю 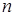, заданное на множестве Z целых чисел: а сравнимо с 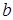по модулю 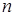(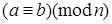) если 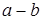делится на 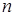. Эквивалентные числа при делении на число 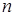дают один и тот же остаток.

5. Отношение «иметь равное значение синуса», определенное на множестве R действительных чисел: 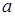~ b, если .

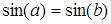6. Отношение «иметь тот же возраст», заданное на множестве всех людей. «Эквивалентные» люди принадлежат к одной и той же возрастной группе.

Приведенные примеры иллюстрируют основное свойство отношения эквивалентности: множество А, на котором задано отношение эквивалентности, разбивается на непустые непересекающиеся подмножества. Все элементы в каждом из таких подмножеств эквивалентны между собой.

В примере 5 в подмножество «группируются» аргументы функции sin, на которых функция sin принимает одно и то же значение. Можно сказать, что «с точки зрения функции sin» аргументы 0 и 9p эквивалентны, так как sin(0)= sin(9p)=0.

В примере 6 подмножества разбиения образуют люди одного возраста.

Дадим строгие определения.

Пусть на множестве А задано отношение эквивалентности и x – произвольный элемент множества А.

Определение. Классом эквивалентности [ х ] элемента х по отношению ~ называют множество всех элементов из А таких, что

[ x ] = { y Î A| (x, y)Î ~ или x ~ y }.

Утверждение.

Классы эквивалентности - непустые множества.

Доказательство.

x ~ x 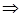(x, x)Î ~ Þ x Î [ x ].

Утверждение.

Если a ~ b, то [ a ] = [ b ].

Доказательство.

1. Пусть x Î [ a ] 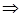x ~ a и a ~ b Þ x ~ b 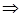x Î [ b ].

2. Пусть x Î [ b ] 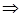x ~ b и b ~ a 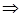x ~ a Þ x Î [ a ].

[ a ] = [ b ].

Утверждение.

Если a ~ b, то [ a ] Ç [ b ] = Æ

Доказательство.

x Î[ a ] Ç [ b ] 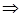x Î [ a ] и x Î [ b ] Þ x ~ a, x ~ b Þ a ~ b Þ противоречие.

Три доказанных утверждения объединяются в одну теорему.

Дата добавления: 2014-01-03