Экстремальные элементы в частично упорядоченном множестве

Решение.

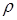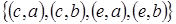= с элементом a не сравнимы элементы b и d. С элементом d не сравнимы элементы a, b, c, e.

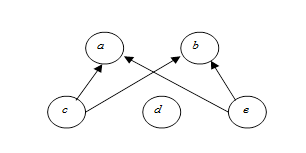
Рис. 2

Пусть М – частично упорядоченное множество. Элемент х 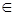М называется минимальным элементом этого множества, если во множестве М не существует элемента a 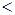x. Элемент y 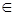М называется максимальным элементом этого множества, если в нем не существует элемента a>y. Минимальный и максимальный элементы в упорядоченных множествах могут существовать, а могут и не существовать (в случае бесконечных множеств), их может быть несколько.

Пример 1.

M = {1, 2 ...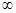 } = N; порядок – обычное сравнение чисел, минимальный элемент - это 1, максимальные элементы отсутствуют).

Пример 2.

M ₁ = [0; 1], M ₂ = (0; 1], M ₃ = [0; 1], M ₄ = (0; 1).

В M ₁ минимальный элемент - это 0, максимальный элемент это - 1.

В M ₂ минимального элемента нет, максимальный элемент - это 1.

В M ₃ минимальный элемент - это 0, максимального элемента нет.

В M ₄ минимальный и максимальный элементы отсутствуют (порядок – обычное сравнение чисел).

Пример 3.

М = {{1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}

Отношение порядка – это отношение включения. В этом множестве три минимальных элемента, не сравнимых между собой, – множества {1;2}, {1; 3}, {2; 3}. Максимальный элемент один – множество {1, 2, 3}.

Пример 4.

М = {2, 3, 4 ... 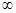}, a < b Û a делит b и a ≠ b.

Максимального элемента нет, а минимальные элементы - все простые числа.

Пример 6.

Покажем, как на диаграмме выглядят минимальный и максимальный элементы в случае множества: М = {2, 3, 4, 6, 7, 12, 16, 18}, a < b Û a делит b и a ≠ b. (рис.3)

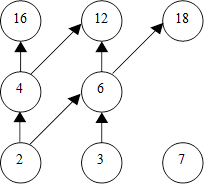
Рис. 3

Минимальные элементы – 2, 3, 7. В минимальный элемент не входит ни одна линия со стрелкой.

Максимальные элементы – 7, 12, 16 18. Из максимального элемента не выходит ни одна линия со стрелкой. Один и тот же элемент может быть одновременно и максимальным, и минимальным. В этом случае он не сравним ни с каким другим элементом данного множества.

Утверждение.

Во всяком непустом конечном, частично упорядоченном множестве М существует хотя бы один минимальный (максимальный) элемент.

Доказательство.

Докажем существование минимального элемента.

Допустим, что в М нет минимальных элементов. Пусть |M| = n, выберем произвольный элемент а Î М, обозначим его через х ₁. Так как х ₁ – не минимальный элемент, то существует b Î М, (обозначим b через x ₂), такой, что x ₂ < х ₁. Далее, существует с Î М, (обозначим с через х ₃), такой, что x ₃ < x ₂ < x ₁. Продолжим перебор элементов множества M. Перебрав все, получим цепочку: x_n < x_{n- 1} <... < x ₂ < x ₁. Так как x_n – не минимальный элемент, то (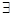k): x_k < x_n, k < n. Таким образом, x_k < x_n < x_{n- 1} <... < x_k <... < < x ₁. Но отношение порядка транзитивно, получаем, что x_k < x_k, - противоречие, строгий порядок антирефлексивен.

Определение. Пусть M – частично упорядоченное множество. Элемент х Î М называется наименьшим элементом множества М, если (" а Î М, a¹x): а > х. Элемент y Î M – наибольшим элементом множества М, если (" а Î М, a¹y): а < y. По определению наименьший (наибольший) элемент сравним со всеми другими элементами множества М

Утверждение.

Если во множестве М существует наименьший (наибольший) элемент, то он единственен.

Доказательство.

Пусть х ₁ ≠ х ₂ – два наименьших элемента множества 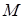. По определению наименьшего элемента х ₁ < х ₂, (х ₁ – наименьший элемент), а также х ₂ < х ₁ – (х ₂ – наименьший элемент) Þ х ₁ = х ₂ в силу антисимметричности любого отношения порядка.

Примеры наибольших и наименьших элементов.

1. Æ и М – являются наименьшим и наибольшим элементами булеана 2 ^М, упорядоченного по включению.

2. В множестве N наименьший элемент - 1, наибольшего элемента нет (порядок – обычное сравнение чисел).

3. Множество R – не имеет ни наибольшего элемента, ни наименьшего элемента (порядок – обычное сравнение чисел).

4. Во множестве В = {{1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}, частично упорядоченном по включению, нет наименьшего элемента; множество

{1, 2, 3} - наибольший элемент множества В.

Дата добавления: 2014-01-03