Геометрическое сглаживание В-сплайнами

Алгоритм Флойда-Стейнберга

Алгоритм заключается в распределении ошибки по соседним пикселам (размазывание) всегда вниз и вправо. Введем понятие порога интенсивности: если интенсивность изображения превышает некую пороговую величину, то пиксел считается белым, иначе — черным. Эту величину обычно устанавливают приблизительно равной половине максимальной интенсивности: T = I _max/2, где T — пороговый параметр или середина диапазона градации, I _max — максимальное число градаций при переходе от черного к белому.

Если I < T, то Р_x (пиксел по х) = черный, ошибка = I — черный,
иначе Р_x (пиксел по х) = белый, ошибка = I — белый.
Пиксел справа: Р_x(x + 1, y) = Р_x(x + 1, y) + 3/8 ошибки.
Пиксел снизу: Р_x(x, y + 1) = Р_x(x, y - 1) + 3/8 ошибки.
Пиксел ниже справа: Р_x(x + 1,y - 1) = Р_x(x + 1,y - 1) + 1/4 ошибки.

В результате в изображении появляются дополнительные точки и исчезают резкие тени.

Любой более или менее сложный чертеж состоит не только из отрезков прямых линий, окружностей и их дуг, но также и из набора кривых линий. Гладкие кривые удобно строить при помощи метода сглаживания кривой типа В-сплайна. Под сплайном (от англ. spline — планка, рейка) обычно понимают агрегатную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. Классический сплайн одной переменной строится так: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.

B-сплайн — это гладкая кривая или, точнее, кривая с непрерывными старшими производными до n-ой, где n — порядок сплайна. Заметим, что линия, составленная из В-сплайнов, не будет проходить точно через заданные точки. Подобную кривую составляют из дуг полиномов третьей степени, так как такой полином обеспечивает необходимую непрерывность. Построение линии происходит с помощью итерационной процедуры.

Рассмотрим построение кубического сплайна. Пусть нам даны две соседние точки, через которые проведем кубический полином, но у полинома — 4 коэффициента, следовательно, нужно еще два дополнительных условия или точки. Для этого прихватим еще две соседние точки. Чем более плавной мы хотим видеть линию, тем сложнее пройти точно через точки. Если в формуле x = q³, то достаточно плавности 3.

Гладкость диктуется физическими задачами, и здесь часто приходится искать компромисс между гладкостью и точностью. Например, гидродинамика работает с поверхностями, которые описываются уравнениями четвертой степени (такой высокий порядок необходим, чтобы повысить гладкость различного рода физических устройств, рассчитанных с помощью этих уравнений, и таким образом избежать завихрений). Но с повышением порядка (то есть гладкости) сплайна точность уменьшается.

Рассмотрим рис. 14.2. Пусть t — параметр, по которому пробегаем от точки P_i к точке P_i+1. При t = 0 мы находимся в точке P_i, при t = 1 — в точке P_i+1. Если 0 < t < 1, то мы находимся между P_i и P_i+1.

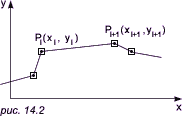
Эта линия в каждой точке имеет систему:

	x(t) = ((a3t + a2)t + a1)t + a0, для 0 <= t <= 1
y(t) = ((b3t + b2)t + b1)t + b0, для 0 <= t <= 1

a₃ = (-x_i-1 + 3x_i - 3x_i+1 + x_i+2)/6
a₂ = (x_i-1 - 2x_i + x_i+1)/2
a₁ = (-x_i-1 + x_i+1)/2
a₀ = (x_i-1 + 4x_i+ x_i+1)/6

Точки b₃ - b₀ расписывают так же, но вместо x подставляют у. Между P_i и P_i+1 точки а и b не меняются. Если после последней точки указать первую точку, то система замкнет контур.

Достоинства В-сплайна: между точками коэффициенты постоянны; локальное изменение не влечет за собой вычисление заново всего сплайна. Недостатки: могут возникать проблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности); с точки зрения эстетики не всегда приемлемы, так как кривизна поверхности, сконструированной с помощью сплайнов, изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).

Дата добавления: 2014-01-03