Определенный интеграл

Перейдем теперь к рассмотрению понятия определенного интеграла, имеющего массу приложений.

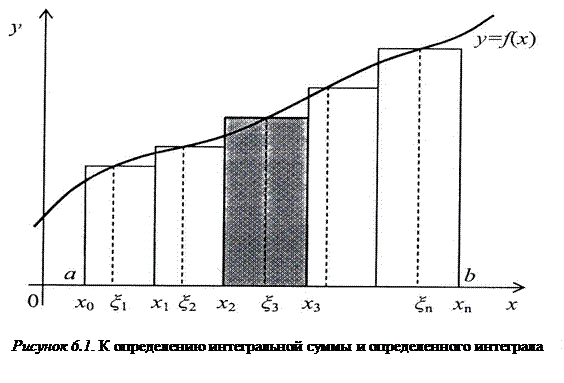Пусть функция y = f(x) определена на отрезке [ a,b ]. Без ограничения общности можно считать, что a < b. Разобьем отрезок [ a,b ] на n частей точками a = x₀ < x₁ < x₂ …< x_n-1 < x_n = b ( см. рис.). Выберем на каждом элементарном отрезке [ x _i-1, x _i] точку ξ_i такую, что x_i-1 < ξ_i < x _i. Обозначим длину отрезка [ x _i-1, x _i] как Δx_i.

Тогда произведение f (ξ_i) Δx_i представляет собой площадь прямоугольника с основанием Δx_i и высотой f (ξ_i), а сумма всех таких произведений — площадь ступенчатой фигуры, тем более близкую к площади под кривой графика y = f(x) на отрезке [ a,b ] (площади криволинейной трапеции), чем мельче разбиение отрезка [ a,b ] на элементарные отрезки [ x _i-1, x _i].

Теперь у нас есть все необходимое для определения определенного интеграла.

Имя Римана — одного из корифеев математики XIX века — фигурирует в этом определении в связи с тем, что в качестве переменной интегрирования здесь используется независимая переменная х. Такое рассмотрение определенного интеграла было введено именно Риманом. В дальнейшем оно было значительно обобщено. Из определения интегрируемости по Риману очевидным образом следует геометрический смысл интеграла как площади криволинейной трапеции, ограниченной сверху графиком функции y = f(x), снизу — отрезком [ a,b ] оси х, справа и слева — соответственно вертикальными прямыми х = а и х = b.

Рассмотрим основные свойства определенного интеграла.

1. Определенный интеграл по отрезку нулевой длины равен нулю:

На невнимательный взгляд прямой связи между первообразной (основой неопределенного интеграла) и римановским определенным интегралом не просматривается — в первом случае это функция, даже множество функций, различаюшихся на произвольную постоянную, во втором — число, выражающее вполне конкретную площадь криволинейной трапеции. Но еще с времен Ньютона и его современника и продолжателя Лейбница эта связь безусловно установлена в виде знаменитой формулы Ньютона-Лейбница.

Есть смысл сформулировать несколько полезных свойств определенного интеграла, также часто используемых в приложениях. Используя их, инженер вправе сказать: я не могу взять любой интеграл, но могу с любой точностью его оценить.

Методы вычисления определенных интегралов ввиду формулы Ньютона-Лейбница аналогичны методам вычисления неопределенных интегралов (непосредственное интегрирование, приведение к виду полного дифференциала, замена переменной, интегрирование по частям). Разбор соответствующих примеров будет проведен на семинаре. Для нас сейчас важнее рассмотреть основные приложения определенного интеграла, демонстрирующие мощь интегрального исчисления.

1.
Вычисление площадей плоских фигур.

В подобных задачах главное — правильно выбрать соответствующую криволинейную трапецию и записать в дифференциальном виде элемент площади. Остальное за нас сделает техника интегрирования. Если вспомнить, как мучительно выводились формулы для площадей плоских фигур в евклидовой геометрии, то применение интегрирования может вызвать глубокую досаду — почему же нам не объяснили этого
сразу?

Похожим способом можно вычислять длину дуги плоской кривой.

Рассмотрим пример.

Интегрирование позволяет с успехом переходить из плоскости в пространство и вычислять площади поверхностей и объемы тел вращения.

Понятие интеграла, как мы видим, может естественным путем переводить нас из одного пространства в другое с более высокой размерностью. Это могучее свойство операции интегрирования получило развитие в виде введения многомерных интегралов, а также использования в качестве переменной определенного интегрирования не независимой переменной х, а произвольной функции, что открывает совершенно новые возможности в функциональном анализе.

Дата добавления: 2014-01-03