Понятие о дифференциальных уравнениях и простейших способах нахождения их решений

Чем выше порядок дифференциального уравнения и чем больше независимых переменных оно содержит, тем большие затруднения вызывает его решение. Поэтому знакомиться с методами решения дифференциальных уравнений естественно с обыкновенных дифференциальных уравнений первого порядка.

Общего способа нахождения решения уравнения первого порядка в аналитическом виде не существует. Теорема Коши является чистой теоремой существования, т.е. она утверждает, что решение существует и единственно, но как его найти, она не предписывает. После Коши многие выдающиеся математики пытались выяснить, можно ли сформулировать общий алгоритм решения дифференциального уравнения первого порядка (хотя бы первого!) подобно тому, как в алгебре решаются системы линейных уравнений, но все усилия привели к тому, что это сделать нельзя. Однако в процессе были найдены способы решения довольно большого числа уравнений первого порядка специального вида, причем к таким уравнениям успешно сводятся многие практические задачи. Их-то мы и рассмотрим.

Наиболее простой и доступный для решения вид — уравнения с разделяющимися переменными.

Принято (несколько жаргонно) называть решение дифференциального уравнения, выраженное в неявном виде, интегралом этого уравнения. Если оказывается возможным разрешить полученное уравнение относительно y, то результатом будет общее решение данного дифференциального уравнения в явном виде.

Все остальные методы решения дифференциальных уравнений первого порядка являются по сути методами приведения данных уравнений к виду с разделяющимися переменными. В первую очередь это относится к однородным дифференциальным уравнениям.

Сначала напомним вспомогательное определение однородной функции.

Как видно, для однородных уравнений способ приведения к уравнениям с разделяющимися переменными достаточно тривиален. Более сложным образом приводятся к разделению переменных линейные уравнения первого порядка.

Линейным уравнением первого порядка называется дифференциальное уравнение вида

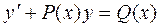
где 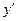и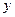входят в первых степенях, не перемножаясь между собой. Если при этом 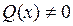, то уравнение называется линейным неоднородным, если 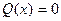, то линейным однородным.

Для дифференциальных уравнений порядка выше первого существуют еще более частные случаи, чем для уравнений первого порядка.

Еще один частный случай, для которого можно получить общее решение уравнения второго порядка — линейные уравнения с постоянными коэффициентами.

Если имеем линейное неоднородное уравнение второго порядка с постоянными коэффициентами, отличающееся от однородного тем, что в правой части стоит функция от х, отличная от нуля, то его решение ищется в виде суммы общего решения однородного уравнения и частного решения неоднородного уравнения (если его каким-то образом удается найти).

Дата добавления: 2014-01-03