Пример: Числа Фибоначчи

Известным примером рекуррентной последовательности второго порядка является последовательность чисел Фибоначчи, для которой 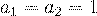, а для : .

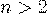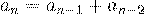Применительно к рекуррентным последовательностям часто ставится задача найти 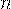-й элемент последовательности.

Для решения этой задачи достаточно хранить в памяти элемент последовательности. Решение задачи разбивается на два основных этапа: начальную установку и продвижение по последовательности.

Для вычисления чисел Фибоначчи первый этап выглядит следующим образом:
a:=1; b:=1
Продвижение по последовательности на один элемент вперед выполняется так:

for k:=3 до n do
begin
c:=a+b;
a:=b;
b:=c;
end;

Каждый из элементов последовательности, начиная с третьего в данном случае, как бы отбирает значение у следующего элемента. Последний элемент, после того как у него отобрали значение, получает новое путем применения рекуррентной формулы. Безвозвратно теряемые старые значения уже не нужны, поскольку на последующие вычисления они повлиять не могут.
Составим алгоритм нахождения n-го числа Фибоначчи с начала до конца:

program fibonacciITER;

var

n, f, a, b, c, k: integer;

begin

writeln (‘Введите число n');

readln (n);

a:=1; b:=1;

for k:=3 to n do

begin

c:=a+b;

a:=b;

b:=c

end;

f:=c;

writeln (n, '-й член последовательности Фибоначчи равен ', f);
end.

В следующей программе числа Фибоначчи вычисляются вначале с использованием итерации, а затем с использованием рекурсии, причем глубина рекурсии отображается. Перед каждым рекурсивным вызовом команда delay(900) приостанавливает вывод глубины рекурсии на 0.9 с.

program fibonacci;

uses crt;

var n,result:integer;

function fibit (n:integer):integer;

var a,b,c,i:integer;

begin

a:= 1; b:= 1;

if (n=1) or (n=2)

then fibit:=1

else begin

for i:= 3 to n do

begin c:=a+b; a:= b; b:=c; write (c,' '); end;

fibit:=c;

writeln;

end;

end;

function fibrek (n:integer):integer;

begin

if (n=1) or (n=2) then fibrek:= 1

else

begin

writeln ('Глубина рекурсии:',n);

delay(900);

fibrek:= fibrek(n-1)+fibrek(n-2);

end;

end;

Дата добавления: 2014-01-03