Применение элементов теории вероятностей к результатам измерений

Из накопленного опыта измерений известно, что при любых измерениях неизбежно появляются случайные погрешности, значение и знак которых при переходе от одного измерения к другому изменяется случайно.

Для приложения теории вероятностей к анализу погрешностей измерений необходимо потребовать, чтобы результаты измерений не содержали грубых и систематических погрешностей. Появление случайной погрешности будем рассматривать как событие, осуществлению которого соответствует определенное значение плотности вероятности, зависящей от погрешности Δ, т. е.

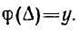(98)

Вероятность попадания значения погрешности внутрь малого промежутка (Δ,Δ+dΔ) или (Δ, Δ—dΔ) пропорциональна величине dΔ:

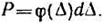(99)

Пусть интервал [-Δ, +Δ] разбит на ряд равных промежутков dΔ, тогда вероятность того, что значение погрешности попадет в любой из этих промежутков по теореме сложения вероятностей равна сумме отдельных вероятностей. Если представить, что число этих промежутков в интервале [-Δ, +Δ] неограниченно возрастает, то dΔ является бесконечно малой величиной, а сумма будет стремиться к интегралу.

Таким образом, вероятность того, что при однократном измерении появится одно из значений случайной погрешности в пределах от -Δ до +Δ равна

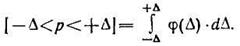(100)

В пределах от минус до плюс бесконечности вероятность появления любого значения погрешности является достоверностью. Поэтому

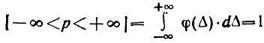(101)

Для определения вида функции φ(Δ используется постулат К. Гаусса о том, что вероятнейшим значением из результатов нес­кольких непосредственных измерений одной и той же величины будет среднее арифметическое значение из этих результатов. При этом плотность вероятностей случайных погрешностей имеет вид

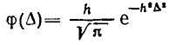(102)

где h — параметр, называемый мерой точности. Известно, что

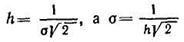(103)

Вероятность того, что погрешность однократного измерения окажется в пределах от Δ до Δ+dΔ из формул (99) и (102) будет

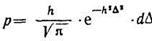(104)

Подставляя (103), получим

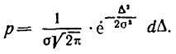(105)

Заменяя Δ= (х—m_х), где m_х — величина, численно равная математическому ожиданию, имеем

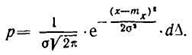(106)

Кривая, построенная по уравнению

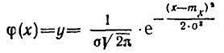(107)

называется кривой нормального распределения вероятностей или кривой Гаусса, изображенной на рис. 6.

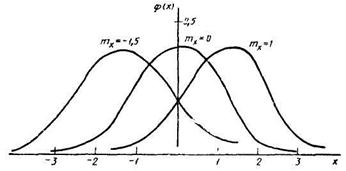
Рис. 6

Для построения графика функции (107) рассмотрим геометрический смысл параметров m_х и σ.

Из формулы (107) видно, что кривая у=φ(х) достигает максимума при х=m_х, причем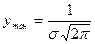. С ростом σ максимальное значение уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом σ кривая растягивается вдоль оси Ох.

На рис. 6 показаны графики нормальных законов при разных m_х, но одинаковых σ, на рис. 7 — наоборот, графики функций у=φ(х) при m_х = 0, но различных σ.

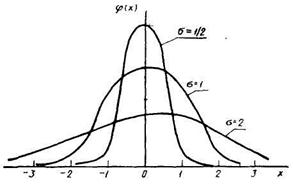
Рис. 7

В практике метрологических работ значительное внимание уделяется определению вероятности попаданию значения измеренных величин в интервал

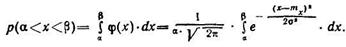(108)

Последнее выражение легко приводится к ранее рассмотренному интегралу Лапласа, для этого выполним замену

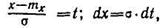(109)

тогда

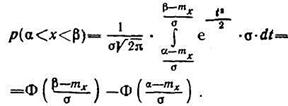(110)

Значения 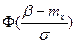и 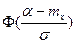находят по таблицам.

В заключение рассмотрим одно важное обстоятельство. Проделаем некоторые числовые расчеты. Положим α=а; β=а+σ, тогда из формулы (110) получим

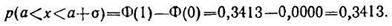
Найдем также

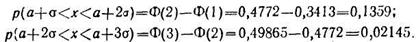
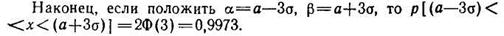
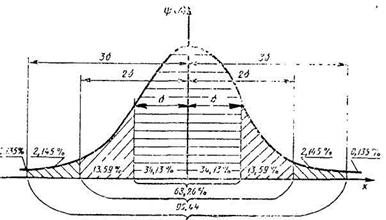
Рис. 8

Последний результат означает, что с вероятностью, близкой к единице (0,9973), случайная величина, подчиняющаяся нормальному закону распределения, не выходит за пределы интервала [а-3σ, а+3σ]. Это утверждение носит название правила трех сигм.

Изучение нормальной кривой показывает, что она определяется некоторыми основными характеристиками, показанными на рис. 8. Очевидно, что 99,73 % площади под кривой лежит в пределах шести средних квадратических отклонений, т. е. по три средних квадратических отклонения в каждую сторону от среднего значения.

Аналогично 95,44 % площади лежит в пределах четырех средних квадратических отклонений и 68,26 % — в пределах двух подобных отклонений. Кроме того, можно заметить, что среднее квадратическое отклонение равно 1/6 размаха.

Описанные характеристики вероятностного распределения важны еще и потому, что они позволяют легко оценивать вероятности появления событий, а также проводить оценку полученных результатов измерений.

Пример. Определить вероятность появления погрешности измерения, абсолютное значение которой окажется в пределах от 4 до 6 мм, т. е. р(4≤Δ≤6), если Δ10 мм.

Решение. Используя формулу (111), можно записать р(4≤Δ≤6) = Ф(4—5/10). Ф(0,1)+Ф(0,1) =0,0398+0,0398 = 0,0796.

Полученное значение необходимо удвоить, так как приведенные в приложении значения даны для половинного интеграла. В итоге получим р(4≤Δ≤6)=2*0,0796=0,1592.

Дата добавления: 2014-01-03