Дисперсия ДСВ: определение, сущность, свойства

Для того чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида:

X
p	0,1	0,8	0,1

Y
p	0,5	0,5

Найдем

М (Х) = 49 · 0,1 + 50 · 0,8 + 51· 0,1 = 50,

М (Y) = 0 · 0,5 + 100 · 0,5 = 50.

Как видно, математические ожидания обеих величин равны, но если для ХМ (Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М (Y). Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.

Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около её математического ожидания. Само слово «дисперсия» означает «рассеивание».

Дисперсия случайной величины обозначается .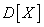

Определение 3. Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

D (Х) = М {[Х – М (Х)] ²}. (6)

Замечание 8. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:

Теорема 1.

D (X) = M (X ²) – M ²(X). (7)

Доказательство. Используя то, что М (Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (6) к виду:

D (X) = M (X – M (X)) ² = M (X ² - 2 X·M (X) + M ²(X)) = M (X ²) – 2 M (X)· M (X) + M ²(X) =

= M (X ²) – 2 M ²(X) + M ²(X) = M (X ²) – M ²(X),

что и требовалось доказать.

Для непосредственного вычисления дисперсии для дискретных величин служит формула:

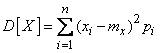. (8)

Очевидно, что дисперсия всегда неотрицательна.

Если обратиться к механической интерпретации распределения, то дисперсия представляет собой не что иное, как момент инерции заданного распределения масс относительно центра тяжести (математического ожидания).

Смысл дисперсии состоит в том, что она характеризует разброс значений случайной величины относительно ее среднего значения.

Введем понятие «центрированной случайной величины».

Пусть имеется случайная величина 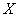с математическим ожиданием 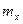. Центрированной случайной величиной, соответствующей величине 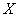, называется отклонение случайной величины 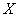от её математического ожидания:

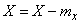. . (9)

Условимся в дальнейшем везде обозначать центрированную случайную величину, соответствующую данной случайной величине, той же буквой со значком наверху.

Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю. Действительно, для прерывной величины

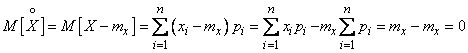. (10)

Центрирование случайной величины, очевидно, равносильно переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию.

Задача 4. Найти дисперсию числа очков, выпавших при бросании игральной кости.

Решение. Ранее было найдено распределение этой случайной величины:

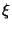
p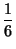

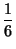
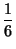
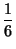
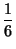
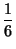
и ее математическое ожидание

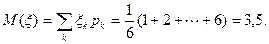
Вычислим дисперсию случайной величины ξ по формуле (8).

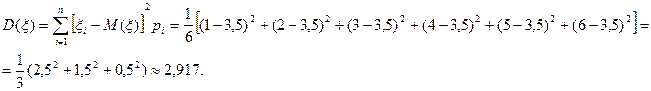
Задача 5. Найти дисперсию случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных.

Решение. Ранее в задаче 1 было найдено распределение этой случайной величины:

Х
р	1/125	12/125	48/125	64/125

и ее математическое ожидание

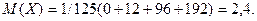
Вычислим значения квадрата отклонения каждого возможного значения от математического ожидания:

(0 – 2,4)² = 5,76; (1 – 2,4)² = 1,96; (2 – 2,4)² = 0,16; (3 – 2,4)² = 0,36.

Следовательно,

D(X) = 5,76.1/125 + 1,96.12/125 + 0,16.48/125 + 0,36.64/125 = 0,48.

Замечание 9. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.

Задача 6. Вычислим дисперсии случайных величин Х и Y, рассмотренных в начале раздела 3.2.2.

D (Х) = (49²·0,1 + 50²·0,8 + 51²·0,1) – 50² = 2500,2 – 2500 = 0,2.

D (Y) = (0²·0,5 + 100²·0,5) – 50² = 5000 – 2500 = 2500.

Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно.

Дата добавления: 2014-01-03