Среднеквадратическое отклонение ДСВ: определение, сущность, свойства

Доказательство.

Доказательство.

Свойства дисперсии

1. Дисперсия постоянной величины С равна нулю:

D (C) = 0. (11)

D (C) = M ((C – M (C)) ²) = M ((C – C) ²) = M (0) = 0.

Следовательно, дисперсия не изменится, если к случайной величине прибавить константу.

2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D (CX) = C ² D (X). (12)

Доказательство.

D (CX) = M ((CX – M (CX)) ²) = M ((CX – CM (X)) ²) = M (C ²(X – M (X)) ²) = C ² D (X).

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

D (X + Y) = D (X) + D (Y). (13)

D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y)) ² =

= M (X ²) + 2 M (X) M (Y) ++ M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) =

= (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.

Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D (X – Y) = D (X) + D (Y). (14)

Доказательство.

D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X).

Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе – «стандартом») случайной величины 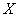. Среднее квадратическое отклонение будем обозначать .

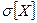Определение 4. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:

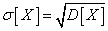. (15)

Для упрощения записей часто пользуются сокращенными обозначениями среднего квадратического отклонения и дисперси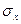и: и 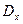. В случае, когда не возникает сомнения, к какой случайной величине относятся эти характеристики, иногда опускают значок «х» у 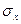и 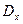и пишут просто σ и D.

Пример 3. В задаче 6 средние квадратические отклонения Х и Y равны соответственно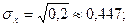

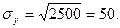
Задача 7. Производится один опыт, в результате которого может появиться или не появиться событие A, вероятность которого равна p. Рассматривается случайная величина X – число появлений события A (характеристическая случайная величина события A). Определить её характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение. Ряд распределения величины A имеет вид:

xi
pi	q	p

где q = 1– p – вероятность непоявления события .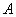

По формуле (1) находим математическое ожидание величины X:

.

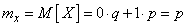Дисперсию величины X определяем по формуле (8):

,

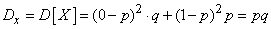откуда

.

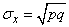Задача 8. Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,4. Случайная величина X – число попаданий. Определить характеристики величины X: математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение. Ряд распределения величины 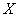имеет вид:

xi
pi	0,216	0,432	0,288	0,064

Вычисляем числовые характеристики величины X:

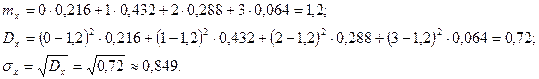
Задача 9. Производится ряд независимых опытов до первого появления события A. Вероятность события A в каждом опыте равна p. Найти дисперсию и среднее квадратическое отклонение числа опытов, которое будет произведено.

Решение. Ряд распределения величины X имеет вид:

xi				…	i	…
pi	p	qp	q^2p	…	q^i-1p	…

В задаче 2 найдено математическое ожидание величины X:

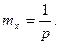
Для определения дисперсии величины X вычислим сначала величину α₂ - второй начальный момент X:

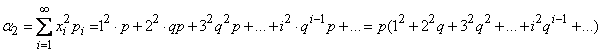Для вычисления ряда, стоящего в скобках, умножим на q ряд:

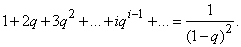
Получим:

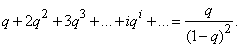
Дифференцируя этот ряд по q, имеем:

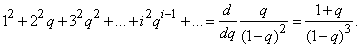
Умножая на 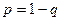, получим:

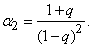
По формуле (7) выразим дисперсию:

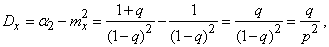
откуда

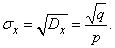
Задача 10. Дан массив из тысячи случайных чисел X, состоящий из единиц с чередованием знака:

1, -1, 1, -1, …, 1, -1.

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение X. Построить график функции распределения.

Дата добавления: 2014-01-03