Физический смысл

Производная второго порядка и ее

Производные второго и вообще высших порядков оказываются существенно необходимыми для определения важных понятий математики, механики, физики и для более полного исследования функций, чем то, которое выполняется с помощью только первой производной.

Так, например, известно, что скорость 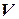движения точки есть производная от пройденного пути 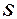по времени 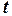, ускорение же 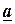есть производная от скорости 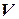по времени

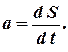
Значит, ускорение является второй производной от пути по времени: 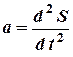, если закон движения 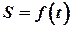. В этом и состоит механический смысл второй производной, (физический смысл).

При вычислении производных высших порядков 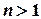процесс отыскания всех производных рассматриваемой функции до данного порядка включительно называется последовательным дифференцированием этой функции.

Вычисление производных 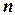-го порядка, при численно заданном 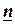, производится по известным формулам и правилам.

Пример.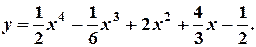

Найти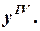

Решение

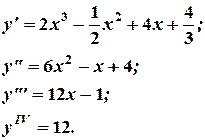
Ясно, что все последующие производные равны тождественно нулю.

Дата добавления: 2014-01-03