Структура решения линейного однородного дифференциального уравнения произвольного порядка

Клиническое значение рефлексов спинного мозга

Название рефлекса	Действие	Центральное звено рефлекса	Ответная реакция
Сухожильные рефлексы
Ахиллов	По Ахиллову сухожилию	S I-II	Подошвенное сгибание стопы
Коленный	По сухожилию четырехглавой мышцы бедра ниже коленной чашечки	L III-IV	Разгибание голени
Локтевой	По сухожилию двуглавой мышцы плеча	C V-VI	Сгибание руки в локтевом суставе
Кожно-мышечные рефлексы
Брюшные рефлексы	Штриховые раздражения
- верхний	параллельно ребрам	Th VIII-IX	Сокращение соответствующих участков брюшной мускулатуры
- средний	на уровне пупка	Th IX-X
- нижний	параллельно паховой складке	Th XII-XII
Кремастерный	В клинической практике используются редко
Анальный

Центрами спинного мозга осуществляется еще ряд рефлексов: сосудодвигательный, дефекационный, мочеиспускательный и др. Они являются вегетативными.

Спинальный шок – возникает при повреждении связей спинного мозга с головным.

Выделяют 2 стадии: 1 стадия – арефлексия, 2 стадия – гиперрефлексия.

Рефлексы спинного мозга находятся под «высшим» контролем структур ствола логовного мозга и коры больших полушарий. Поэтому разрушение связи спинного и головного мозга вызывает абсолютную дисфункцию спинного мозга – спинальный шок.

Линейным однородным дифференциальным уравнением 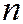–го порядка называется уравнение

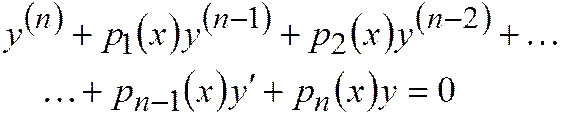(2.14.1)

или

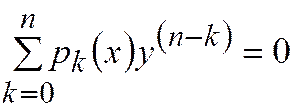(2.14.2)

Здесь 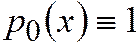, под однородностью понимается равенство левой части нулю.

Очевидно, что если 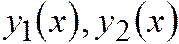– частные решения уравнений (2.14.1), (2.14.2), то функци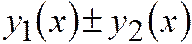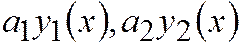и , и 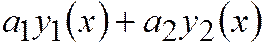тоже будут решениями этих уравнений.

Теорема (о структуре общего решения линейного однородного уравнения).

Если 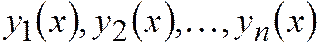– линейно независимые частные решения линейного однородного уравнения 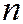–го порядка, то его общее решение можно представить в виде

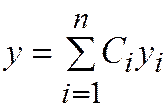. (2.14.3)

Доказательство:

Очевидно, что в силу линейной структуры уравнения (2.14.2) функция (2.14.3) является решением уравнения кА линейная комбинация частных решений.

Покажем, что с помощью формулы (2.14.3) можно решить любую задачу Коши.

Рассмотрим произвольные начальные условия

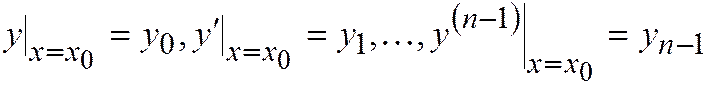. (2.14.4)

Подставляя функцию (2.14.3) в условия (2.14.4), получаем линейную систему уравнений

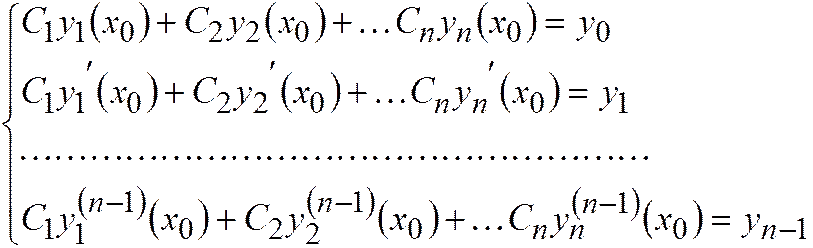(2.14.5)

для вычисления значений 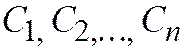. Главным определителем системы (2.14.5) является определитель Вронского

.

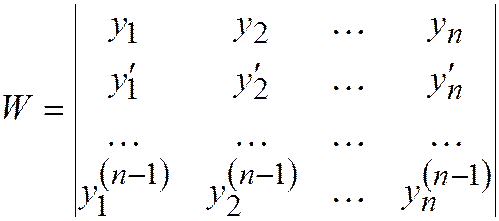в точке 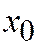. Так как система функций 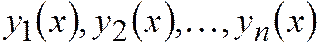является линейно независимой, то определитель Вронского отличен от нуля, следовательно система (2.14.5) имеет единственное решение. Таким образом, мы решили произвольную задачу Коши, что и требовалось доказать.

Дата добавления: 2014-01-03