Лекция №6. Объектом исследования служит неподвижный монокристалл

Метод Лауэ.

1. Экспериментальная схема.

Объектом исследования служит неподвижный монокристалл. Используется излучение со сплошным спектром. Внешний вид устройства-камеры для съемки лауэграмм приведен на рисунке 6.1 (а,б). На схеме показаны основные узлы камеры:

1. Коллимационное устройство, формирующее квазипараллельный пучок рентгеновских лучей.

2. Образец монокристалл.

3. Гониометрическая головка, обеспечивающая возможность поворота монокристалла вокруг трех взаимно перпендикулярных осей, пересекающихся в одной точке.

4. Кассеты с пленкой для регистрации дифракционной картины при съемке "на просвет" - лауэграммы или на отражение - эпиграммы.

2. Назначение метода - определение симметрии и ориентировки монокристалла.

3. Симметрия дифракционных картин - лауэграмм.

Симметрия дифракционных картин, в соответствии с принципом Кюри, отвечает симметрии кристалла при наблюдении его вдоль оси пучка рентгеновских лучей. Если, например, вдоль пучка проходит плоскость симметрии, то кроме некоторого семейства плоскостей (h_i) наклоненного к пучку под углом Брэгга для какой либо длины волны, то также наклонено еще одно семейство плоскостей, связанное с первым операцией симметрии. Эти два семейства дадут два симметрично расположенных дифракционных пятна на фотопластинке. Семейства плоскостей связанные операцией симметрии структурно идентичны. Длины волн лучей отраженных ими будут одинаковы. Поэтому и яркость пятен должна быть одинакова. На рентгенограмме в целом возникает линия симметрии, проходящая через центр первичного пучка. На рис. 6.2 приведены возможные типы симметрии лауэграмм. Если направление пучка не совпадает ни с одним из возможных элементов симметрии, то лауэграмма полностью асимметрична. Если вдоль пучка оси 2-го, 3-го, 4-го и 6-го порядков то и симметрия лауэграмм - 2,3,4,6 и т.д.

Точечная группа кристаллов по их огранке определяется недостаточно однозначно. Поэтому лучше ее определять, опираясь на внутриатомное строение кристаллов. Для выявления точечной группы привлекается симметрия дифракционных картин. Точечная группа определяет симметрию в расположении семейств атомных плоскостей. При этом простые оси или винтовые, зеркальные плоскости или плоскости скользящего отражения симметрия дифракционных картин одинакова. На рис. 6.3 (а,б) приведены структуры с осью 2 и 2₁. В обоих случаях семейства плоскостей с межплоскостным расстоянием d одинаковы и состоят из одинаковых двойных плоскостей отстоящих на расстояние s друг от друга. Очевидно, что семейства связанные операцией симметрии отражают рентгеновские лучи под одинаковыми углами Брэгга, и отраженные лучи будут иметь одинаковую интенсивность.

Симметрию, определенную на основании этих двух признаков называют дифракционной симметрией. Однако симметрия дифракционная не совпадает с точечной группой кристалла.

Рассмотрим пример отражения от плоскосте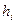й () и (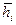) т.е. с разных сторон от этой плоскости (рис. 6.4). Отражения будут при одинаковых углах скольжения и с одинаковой интенсивностью независимо от того есть центр симметрии или нет. Действительно при отражении от семейства изображенного вверху плоскость из черных кружочков отражает с отставанием по фазе от плоскости из белых кружочков, а на нижней части рисунка наоборот. Но разность фаз одинакова, поэтому и суммарные амплитуды отраженных лучей одинаковы. Это является следствием закона центросимметричности дифракционного эффекта (закон Фриделя). В отношении дифракции рентгеновских лучей в общем случае кристалл обладает центром инверсии. То есть дифракционная симметрия кристалла выше, чем его точечная группа симметрии. Она отвечает точечной группе плюс центр симметрии и равнодействующие элементы симметрии. Так кристаллы, принадлежащие к точечным группам m, 2 и 2/m принадлежат к одному дифракционному классу. В таблице 1 приведено распределение точечных групп по дифракционным классам симметрии (Лауэ-класс симметрии). Однако существует ситуация когда закон Фриделя нарушается. Это происходит в тех случаях, когда велики поправки на аномальную дисперсию (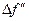). Нарушение закона Фриделя происходит вследствие изменения фазы 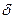атомной амплитуды рассеяния. Примером может служить отражение от А и В поверхностей кристаллов с решеткой сфалерита для отражений с нечетными индексами (см. задачу 4.7 [ ]). Закон центросимметричности дифракционных картин накладывает ограничения на возможность определения точечной группы симметрии кристалла, однако преодолеваемые на следующих этапах анализа структуры (анализ законов погасаний, анализ интенсивностей отражений). Анализ физических свойств, таких как пьезоэффект, пироэффект, анализ фигур травления и т.п. Все это является существенным дополнением к дифракционным данным, позволяющим во многих случаях однозначно установить класс симметрии кристалла. Анализ симметрии не требует индицирования лауэграмм. Однако, для определения ориентировки кристаллов необходим более детальный анализ лауэграмм.

4. Закономерности расположения рефлексов на лауэграммах.

Для выявления закономерностей расположения рефлексов воспользуемся построением Эвальда преобразовав его применительно к методу Лауэ. Это вызвано тем, что используется полихроматическое излучение.

Радиус сферы Эвальда равный 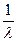умножим на 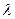. В этом случае это безразмерный радиус равный 1.

При таком подходе векторы ОР необходимо так же преобразовать. Масштаб длин векторов нужно изменить умножив их на 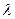. И так как в спектре есть непрерывный набор длин волн от 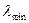до 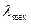, то узлы обратной решетки превратятся в эффективные отрезки, длина которых 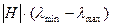. В отражающем положении для длин волн из указанного интервала окажутся те плоскости, для которых эффективные отрезки пересекут сферу Эвальда. Очевидно, что одному узловому направлению а ОР на лауэграммах (эпиграммах) отвечает один рефлекс. То есть отражения разных порядков от одной системы плоскостей 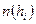где n = 1,2,3… дадут одно пятно, так как если эффективные отрезки для разных узлов данного узлового направления перекрываются так, что в точке пересечения со сферой проходят отрезки, отвечающие разным узлам, то в одном пятне накладываются отражения разных порядков от одной и той же системы плоскостей.

Пусть ось зоны плоскостей 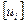составляет с первичным пучком угол 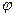. Соответствующая ей плоскость ОР, проходящая через нулевой узел, перпендикулярная оси зоны, пересекает сферу по окружности радиусом 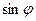. Эффективные отрезки для узлов этой плоскости пересекают эту окружность. Очевидно, что интерференционные максимумы для плоскостей попадающих в отражающее положение будут распологаться в направлении образующих конуса с углом полураствора 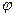. Пересечение этой конической поверхности с фотопластинками, перпендикулярными оси первичного пучка, образуют кривые второго порядка: при 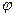<45⁰ - эллипсы, при 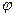=45⁰ - параболы, при 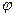>45⁰ - гиперболы, при 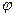=90⁰ - прямые. Все эти кривые для лауэграмм проходят через след первичного пучка. Для эпиграмм 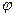>45⁰ и гиперболы не проходят через след первичного пучка, а проходят только прямые. На этих кривых и распологаются рефлексы отражений от плоскостей отдельных зон (рис. 6 а,б лауэграмма (а) и эпиграмма (б)). Плоскость решетки кристалла принадлежит нескольким зонам. Этой плоскости отвечает узловое направление в ОР следовательно соответствующее ему пятно в принципе может быть точкой пересечения нескольких зональных кривых. Если плоскость решетки кристалла параллельна первичному пучку, то каждое кристаллографическое направление, лежащее в этой плоскости может быть осью зоны плоскостей. Соответствующие плоскости ОР будут наклонены к пучку под разными углами. Это приводит к возникновению зональных кривых "вложенных" друг в друга, касающихся в центральной точке лауэграммы и имеющих общую линию симметрии.

5. Связь между лауэграммой (эпиграммой) и гномостереографической проекцией кристалла.

Для определения ориентировки кристалла в лабораторной системе координат (плоскость xy параллельна плоскости проекции нормальной к падающему пучку, а ось z параллельна пучку) необходимо построить гномостереографическую проекцию отражающих плоскостей.

Рис. 6.7 (а,б) показывает связь между положением рефлекса на фотопластинке, нормалью к отражающим плоскостям и первичным пучком. Все они лежат в одной плоскости. Из рисунка видно, что если расстояние от центра рентгенограммы до рефлекса l, а расстояние от кристалла до фотопластинки L, то 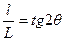для лауэграммы и 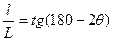для эпиграммы.

Нормали к плоскостям зоны расположены в одной плоскости, проходящей через центр сферы. Поэтому проекции плоскостей одной зоны, давших отражение на одну зональную кривую, лежат на одном меридиане. Точка, удаленная от этого меридиана на 90⁰ является проекцией оси зоны.

6. Определение ориентировки кристаллов проводится на основе анализа гномостереографических проекций построенных по рентгенограммам Лауэ.

Для анализа удобно пользоваться понятиями "важных" направлений и "важных" зон. "Важными" принято называть узловые направления и соответствующие им узловые сетки ОР: <100>, <110>, <111>. Наконец, "важными" можно считать и направления, индексы которых содержат только нули, единицы и двойки и т.д.

На рентгенограммах Лауэ "важным" осям зон отвечают соответствующие "важные" зональные кривые. Плотность рефлексов на таких кривых максимальна (рис. 6.6). так как узлы между "важными" осями зон не могут быть малыми то "важные" зональные кривые окружены слепым пятном, т.е. располагаются на больших расстояниях друг от друга, чем "вложенные" кривые менее важных зон (рис. 6.6). Важные рефлексы, так же окружены слепым пятном, так же принадлежат нескольким "важным" зональным кривым. Иногда "важный" рефлекс может даже отсутствовать, но пересечение зональных кривых и слепое пятно свидетельствует, что в этом месте должно проходить "важное" узловое направление ОР.

Анализ гномостереографических проекций, построенным по рентгенограммам Лауэ, позволяет определить ориентировку кристаллов. Сначала следует выяснить нет ли закономерностей на лауэграмме, указывающих на расположение элементов симметрии относительно первичного пучка. При этом следует учитывать и такую ситуацию когда элементы симметрии лишь приблизительно параллельны или перпендикулярны оси пучка. Если же кристалл находится в общем положении то анализ производится по разному для кристаллов с известной решеткой и в общем случае, когда решетка не известна.

В случае когда решетка известна достаточно проиндицировать несколько важных осей зон - кристаллографических направлений и важных рефлексов - нормалей к плоскостям с малыми индексами. Индицирование можно провести по углам между осями зон. Можно проиндицировать так же и важные нормали (им отвечают рефлексы на зональных кривых). Важное узловое направление [h_i] в ОР принадлежащее двум важным зональным кривым с осям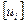и и 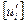, можно использовать для индицирования так как

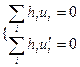откуда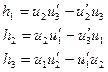

Сопоставляя расчетные углы между осями зон и векторами ОР (h_i) принадлежащими разным зонам можно однозначно проиндицировать кристаллографические направления - оси зон и отражающие плоскости - рефлексы. Расположения этих элементов в системе координат лауэграммы позволяет установить ориентацию кристалла. Если решетка кристалла не известна то для ориентировки кристалла сначало надо учитывать его сингонию, затем наметить координатные оси и проиндицировать рентгенограмму, установив ориентацию важных нормалей или осей зон в системе координат рентгенограммы.

Для определения сингонии кристалла необходимо получить несколько рентгенограмм при фиксированных поворотах кристалла относительно внешних осей. Выделив в сумме 10-15 "важных" осей зон и столько же важных нормалей, являющихся пересечением зональных кривых на отдельных рентгенограммах, перенесем их на сводную гномостереографическую проекцию.

В кристаллах разных сингоний взаимное положение важных нормалей и важных осей зон различно. В таблице приведены взаимные расположения нормалей к важным плоскостям и осей важных зон.

Из таблицы видно, что у кристаллов кубической сингонии любое кристаллографическое направление с индексами [h_i] совпадает с нормалью к плоскости (h_i). То есть по всему полю гномостереографической проекции в пределах точности ~1⁰ оси зон будут совпадать с полюсами плоскостей.

В кристаллах средних сингоний только направления [001] и [h₁ h₂ 0] совпадают с нормалями к плоскостям с теми же индексами, т.е. на меридиане перпендикулярном оси [001] совпадают направления [h₁ h₂ 0] и полюса плоскостей (h₁ h₂ 0). Совмещая ось [001] с осью пучка получим симметрию оси 4-го порядка для тетрагональной, 6-го для гексагональной и 3-го для тригональной сингоний.

В кристаллах ромбической сингонии оси и нормали лежат на одних и тех же дугах большого круга, соответствующих особым плоскостям. Эти три дуги пересекаются под прямыми углами и точки пересечения их являются осями решетки. В решетке моноклинных кристаллов есть только одна нормаль и направление [010] совпадающее с ней. На дуге большого круга перпендикулярной этому направлению - оси 2 лежат направления [h₁ 0 h₃] и полюса плоскостей (h₁ h₂ 0). В моноклинной решетке выбор осей а₂ и а₃ следует брать так чтобы ячейка оказалась примитивной с минимальными периодами идентичности вдоль этих осей.

В триклинной решетке совпадений нет.

Дата добавления: 2014-01-03